Page 283 - Advanced Thermodynamics for Engineers, Second Edition

272 CHAPTER 12 CHEMICAL EQUILIBRIUM AND DISSOCIATION

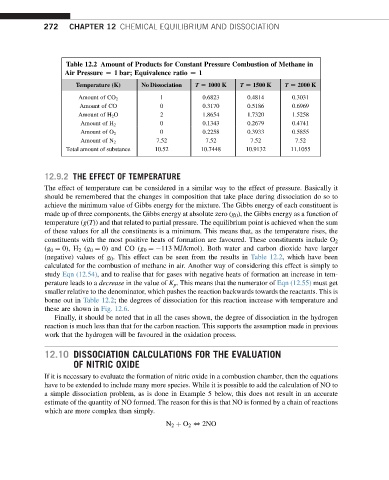
Table 12.2 Amount of Products for Constant Pressure Combustion of Methane in
Air Pressure [ 1 bar; Equivalence ratio [ 1
Temperature (K) No Dissociation T [ 1000 K T [ 1500 K T [ 2000 K

Amount of CO 2 1 0.6823 0.4814 0.3031
Amount of CO 0 0.3170 0.5186 0.6969
Amount of H 2 O 2 1.8654 1.7320 1.5258
0 0.1343 0.2679 0.4741
Amount of H 2
0 0.2258 0.3933 0.5855
Amount of O 2
7.52 7.52 7.52 7.52
Amount of N 2
Total amount of substance 10.52 10.7448 10.9132 11.1055

12.9.2 THE EFFECT OF TEMPERATURE
The effect of temperature can be considered in a similar way to the effect of pressure. Basically it
should be remembered that the changes in composition that take place during dissociation do so to
achieve the minimum value of Gibbs energy for the mixture. The Gibbs energy of each constituent is
made up of three components, the Gibbs energy at absolute zero (g 0 ), the Gibbs energy as a function of
temperature (g(T)) and that related to partial pressure. The equilibrium point is achieved when the sum
of these values for all the constituents is a minimum. This means that, as the temperature rises, the
constituents with the most positive heats of formation are favoured. These constituents include O 2
(g 0 ¼ 0), H 2 (g 0 ¼ 0) and CO (g 0 ¼ 113 MJ/kmol). Both water and carbon dioxide have larger
(negative) values of g 0 . This effect can be seen from the results in Table 12.2, which have been
calculated for the combustion of methane in air. Another way of considering this effect is simply to
study Eqn (12.54), and to realise that for gases with negative heats of formation an increase in tem-
perature leads to a decrease in the value of K p . This means that the numerator of Eqn (12.55) must get
smaller relative to the denominator, which pushes the reaction backwards towards the reactants. This is
borne out in Table 12.2; the degrees of dissociation for this reaction increase with temperature and
these are shown in Fig. 12.6.
Finally, it should be noted that in all the cases shown, the degree of dissociation in the hydrogen
reaction is much less than that for the carbon reaction. This supports the assumption made in previous
work that the hydrogen will be favoured in the oxidation process.

12.10 DISSOCIATION CALCULATIONS FOR THE EVALUATION
OF NITRIC OXIDE

If it is necessary to evaluate the formation of nitric oxide in a combustion chamber, then the equations
have to be extended to include many more species. While it is possible to add the calculation of NO to
a simple dissociation problem, as is done in Example 5 below, this does not result in an accurate
estimate of the quantity of NO formed. The reason for this is that NO is formed by a chain of reactions
which are more complex than simply.
N 2 þ O 2 5 2NO