Page 300 - Advanced Thermodynamics for Engineers, Second Edition

12.12 CONCLUDING REMARKS 289

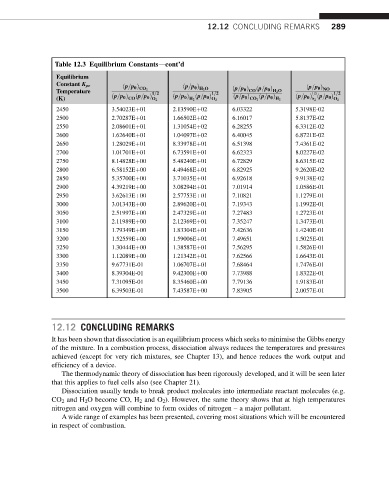
Table 12.3 Equilibrium Constantsdcont’d
Equilibrium
Constant K pr
ðp=p 0 Þ ðp=p 0 Þ H 2 O ðp=p 0 Þ NO
Temperature CO 2 1=2 1=2 ðp=p 0 Þ CO ðp=p 0 Þ H 2 O 1=2 1=2
(K) ðp=p 0 Þ CO ðp=p 0 Þ O 2 ðp=p 0 Þ ðp=p 0 Þ O 2 ðp=p 0 Þ CO 2 ðp=p 0 Þ H 2 ðp=p 0 Þ ðp=p 0 Þ O 2
H 2
N 2
2450 3.54023Eþ01 2.13590Eþ02 6.03322 5.3198E-02
2500 2.70287Eþ01 1.66502Eþ02 6.16017 5.8137E-02
2550 2.08601Eþ01 1.31054Eþ02 6.28255 6.3312E-02
2600 1.62640Eþ01 1.04097Eþ02 6.40045 6.8721E-02
2650 1.28029Eþ01 8.33978Eþ01 6.51398 7.4361E-02
2700 1.01701Eþ01 6.73591Eþ01 6.62323 8.0227E-02
2750 8.14828Eþ00 5.48240Eþ01 6.72829 8.6315E-02
2800 6.58152Eþ00 4.49468Eþ01 6.82925 9.2620E-02
2850 5.35700Eþ00 3.71035Eþ01 6.92618 9.9138E-02
2900 4.39219Eþ00 3.08294Eþ01 7.01914 1.0586E-01
2950 3.62613Eþ00 2.57753Eþ01 7.10821 1.1279E-01
3000 3.01343Eþ00 2.89620Eþ01 7.19343 1.1992E-01
3050 2.51997Eþ00 2.47329Eþ01 7.27483 1.2723E-01
3100 2.11989Eþ00 2.12369Eþ01 7.35247 1.3473E-01
3150 1.79349Eþ00 1.83304Eþ01 7.42636 1.4240E-01
3200 1.52559Eþ00 1.59006Eþ01 7.49651 1.5025E-01
3250 1.30444Eþ00 1.38587Eþ01 7.56295 1.5826E-01
3300 1.12089Eþ00 1.21342Eþ01 7.62566 1.6643E-01
3350 9.67731E-01 1.06707Eþ01 7.68464 1.7476E-01
3400 8.39304E-01 9.42300Eþ00 7.73988 1.8322E-01
3450 7.31095E-01 8.35460Eþ00 7.79136 1.9183E-01
3500 6.39503E-01 7.43587Eþ00 7.83905 2.0057E-01

12.12 CONCLUDING REMARKS
It has been shown that dissociation is an equilibrium process which seeks to minimise the Gibbs energy
of the mixture. In a combustion process, dissociation always reduces the temperatures and pressures
achieved (except for very rich mixtures, see Chapter 13), and hence reduces the work output and
efficiency of a device.
The thermodynamic theory of dissociation has been rigorously developed, and it will be seen later
that this applies to fuel cells also (see Chapter 21).
Dissociation usually tends to break product molecules into intermediate reactant molecules (e.g.
CO 2 and H 2 O become CO, H 2 and O 2 ). However, the same theory shows that at high temperatures
nitrogen and oxygen will combine to form oxides of nitrogen – a major pollutant.
A wide range of examples has been presented, covering most situations which will be encountered
in respect of combustion.