Page 84 - Advanced engineering mathematics

64 CHAPTER 2 Linear Second-Order Equations

EXAMPLE 2.19 Critical Damping
−t
Let c = 2 and k = m = 1. Then y(t) = (c 1 + c 2 t)e . Suppose the bob is initially pulled up four
feet above the equilibrium position and then pushed downward with a speed of 5 feet per second.
Then y(0) =−4, and y (0) = 5. So

−t
y(t) = (−4 + t)e .
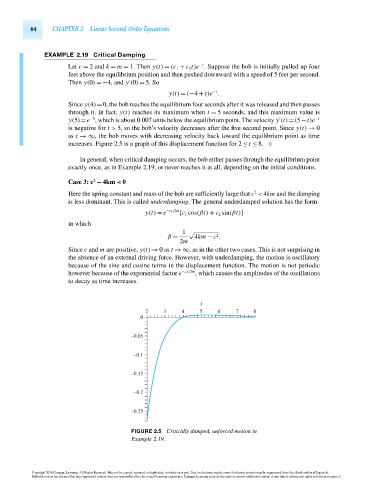
Since y(4)=0, the bob reaches the equilibrium four seconds after it was released and then passes
through it. In fact, y(t) reaches its maximum when t = 5 seconds, and this maximum value is
−5

y(5)=e , which is about 0.007 units below the equilibrium point. The velocity y (t)=(5−t)e −t
is negative for t > 5, so the bob’s velocity decreases after the five second point. Since y(t) → 0
as t →∞, the bob moves with decreasing velocity back toward the equilibrium point as time
increases. Figure 2.5 is a graph of this displacement function for 2 ≤ t ≤ 8.
In general, when critical damping occurs, the bob either passes through the equilibrium point
exactly once, as in Example 2.19, or never reaches it at all, depending on the initial conditions.

2
Case 3: c − 4km < 0
Here the spring constant and mass of the bob are sufficiently large that c <4km and the damping
2
is less dominant. This is called underdamping. The general underdamped solution has the form
y(t) = e −ct/2m [c 1 cos(βt) + c 2 sin(βt)]
in which
1 √
2
β = 4km − c .
2m
Since c and m are positive, y(t)→0as t →∞, as in the other two cases. This is not surprising in
the absence of an external driving force. However, with underdamping, the motion is oscillatory
because of the sine and cosine terms in the displacement function. The motion is not periodic
however because of the exponential factor e −ct/2m , which causes the amplitudes of the oscillations
to decay as time increases.

t
2 3 4 5 6 7 8
0

–0.05

–0.1

–0.15

–0.2

–0.25

FIGURE 2.5 Critically damped, unforced motion in
Example 2.19.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:12 THM/NEIL Page-64 27410_02_ch02_p43-76