Page 87 - Advanced engineering mathematics

2.4 Spring Motion 67

1
1

0.5
0.5

0
2 4 6 8 10 12 0
t 5 10 15 20
t
–0.5
–0.5

–1
–1
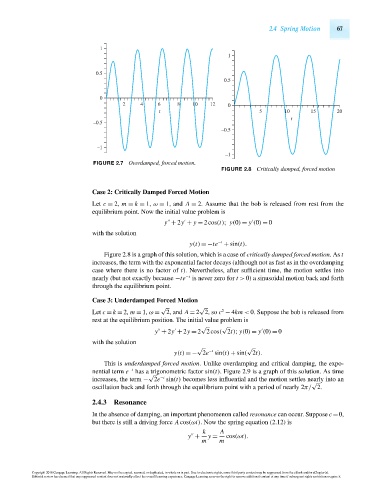
FIGURE 2.7 Overdamped, forced motion.
FIGURE 2.8 Critically damped, forced motion

Case 2: Critically Damped Forced Motion
Let c = 2, m = k = 1, ω = 1, and A = 2. Assume that the bob is released from rest from the
equilibrium point. Now the initial value problem is

y + 2y + y = 2cos(t); y(0) = y (0) = 0

with the solution
−t
y(t) =−te + sin(t).
Figure 2.8 is a graph of this solution, which is a case of critically damped forced motion.As t
increases, the term with the exponential factor decays (although not as fast as in the overdamping
case where there is no factor of t). Nevertheless, after sufficient time, the motion settles into
nearly (but not exactly because −te −t is never zero for t > 0) a sinusoidal motion back and forth
through the equilibrium point.

Case 3: Underdamped Forced Motion
√ √
2
Let c = k = 2, m = 1, ω = 2, and A = 2 2, so c − 4km < 0. Suppose the bob is released from
rest at the equilibrium position. The initial value problem is
√ √

y + 2y + 2y = 2 2cos( 2t); y(0) = y (0) = 0

with the solution
√ √
−t
y(t) =− 2e sin(t) + sin( 2t).
This is underdamped forced motion. Unlike overdamping and critical damping, the expo-
nential term e −t has a trigonometric factor sin(t). Figure 2.9 is a graph of this solution. As time
√
−t
increases, the term − 2e sin(t) becomes less influential and the motion settles nearly into an
√
oscillation back and forth through the equilibrium point with a period of nearly 2π/ 2.
2.4.3 Resonance
In the absence of damping, an important phenomenon called resonance can occur. Suppose c=0,
but there is still a driving force A cos(ωt). Now the spring equation (2.12) is
k A

y + y = cos(ωt).
m m

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:12 THM/NEIL Page-67 27410_02_ch02_p43-76