Page 90 - Advanced engineering mathematics

70 CHAPTER 2 Linear Second-Order Equations

0.8

0.4

0
4 8 12 16
t
–0.4

–0.8

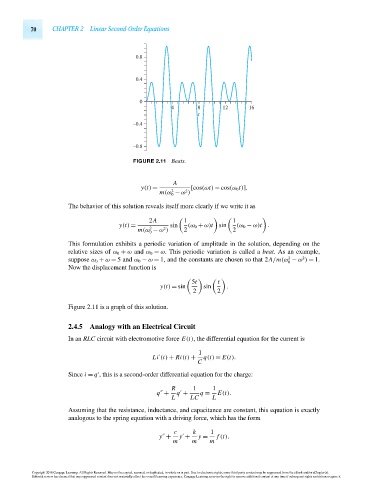
FIGURE 2.11 Beats.

A
y(t) = [cos(ωt) − cos(ω 0 t)].
2
m(ω − ω )
2
0
The behavior of this solution reveals itself more clearly if we write it as
2A 1 1
y(t) = sin (ω 0 + ω)t sin (ω 0 − ω)t .
2
m(ω − ω ) 2 2
2
0
This formulation exhibits a periodic variation of amplitude in the solution, depending on the
relative sizes of ω 0 + ω and ω 0 − ω. This periodic variation is called a beat. As an example,
2
2
suppose ω 0 + ω = 5 and ω 0 − ω = 1, and the constants are chosen so that 2A/m(ω − ω ) = 1.
0
Now the displacement function is
5t t

y(t) = sin sin .
2 2
Figure 2.11 is a graph of this solution.

2.4.5 Analogy with an Electrical Circuit

In an RLC circuit with electromotive force E(t), the differential equation for the current is
1

Li (t) + Ri(t) + q(t) = E(t).
C
Since i = q , this is a second-order differential equation for the charge:

R 1 1

q + q + q = E(t).
L LC L
Assuming that the resistance, inductance, and capacitance are constant, this equation is exactly
analogous to the spring equation with a driving force, which has the form

c k 1

y + y + y = f (t).
m m m

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:12 THM/NEIL Page-70 27410_02_ch02_p43-76