Page 89 - Advanced engineering mathematics

2.4 Spring Motion 69

20

15
10

5
0
5 10 15 20
–5 t

–10
–15

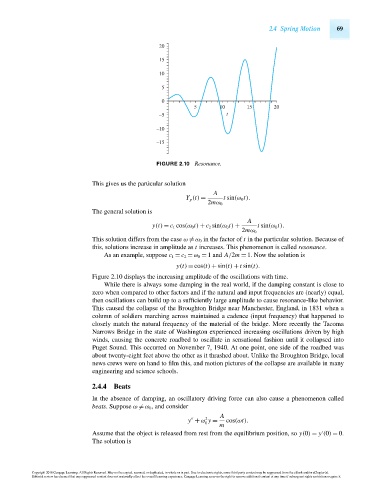
FIGURE 2.10 Resonance.

This gives us the particular solution
A
Y p (t) = t sin(ω 0 t).
2mω 0
The general solution is
A
y(t) = c 1 cos(ω 0 t) + c 2 sin(ω 0 t) + t sin(ω 0 t).
2mω 0
This solution differs from the case ω = ω 0 in the factor of t in the particular solution. Because of
this, solutions increase in amplitude as t increases. This phenomenon is called resonance.
As an example, suppose c 1 = c 2 = ω 0 = 1 and A/2m = 1. Now the solution is
y(t) = cos(t) + sin(t) + t sin(t).
Figure 2.10 displays the increasing amplitude of the oscillations with time.
While there is always some damping in the real world, if the damping constant is close to
zero when compared to other factors and if the natural and input frequencies are (nearly) equal,
then oscillations can build up to a sufficiently large amplitude to cause resonance-like behavior.
This caused the collapse of the Broughton Bridge near Manchester, England, in 1831 when a
column of soldiers marching across maintained a cadence (input frequency) that happened to
closely match the natural frequency of the material of the bridge. More recently the Tacoma
Narrows Bridge in the state of Washington experienced increasing oscillations driven by high
winds, causing the concrete roadbed to oscillate in sensational fashion until it collapsed into
Puget Sound. This occurred on November 7, 1940. At one point, one side of the roadbed was
about twenty-eight feet above the other as it thrashed about. Unlike the Broughton Bridge, local
news crews were on hand to film this, and motion pictures of the collapse are available in many
engineering and science schools.
2.4.4 Beats

In the absence of damping, an oscillatory driving force can also cause a phenomenon called
beats. Suppose ω = ω 0 , and consider
A
2
y + ω y = cos(ωt).
0
m
Assume that the object is released from rest from the equilibrium position, so y(0) = y (0) = 0.

The solution is

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:12 THM/NEIL Page-69 27410_02_ch02_p43-76