Page 341 - Advanced thermodynamics for engineers

330 CHAPTER 15 COMBUSTION AND FLAMES

T T T
Preheat zone Reaction zone
Mass flow

indicates thermal energy flow

Concentration or temperature Concentration T Temperature
of reactants

T

T

Distance
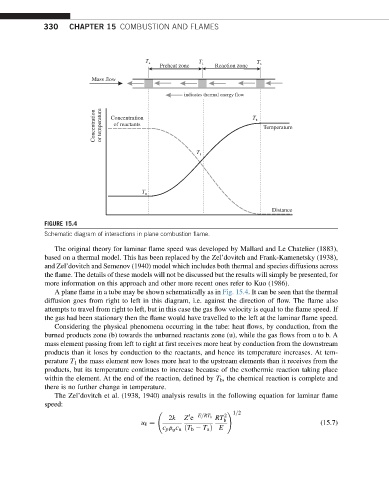
FIGURE 15.4
Schematic diagram of interactions in plane combustion flame.
The original theory for laminar flame speed was developed by Mallard and Le Chatelier (1883),
based on a thermal model. This has been replaced by the Zel’dovitch and Frank-Kamenetsky (1938),
and Zel’dovitch and Semenov (1940) model which includes both thermal and species diffusions across
the flame. The details of these models will not be discussed but the results will simply be presented, for
more information on this approach and other more recent ones refer to Kuo (1986).
A plane flame in a tube may be shown schematically as in Fig. 15.4. It can be seen that the thermal
diffusion goes from right to left in this diagram, i.e. against the direction of flow. The flame also
attempts to travel from right to left, but in this case the gas flow velocity is equal to the flame speed. If
the gas had been stationary then the flame would have travelled to the left at the laminar flame speed.
Considering the physical phenomena occurring in the tube: heat flows, by conduction, from the
burned products zone (b) towards the unburned reactants zone (u), while the gas flows from u to b. A
mass element passing from left to right at first receives more heat by conduction from the downstream
products than it loses by conduction to the reactants, and hence its temperature increases. At tem-
perature T 1 the mass element now loses more heat to the upstream elements than it receives from the
products, but its temperature continues to increase because of the exothermic reaction taking place
within the element. At the end of the reaction, defined by T b , the chemical reaction is complete and
there is no further change in temperature.
The Zel’dovitch et al. (1938, 1940) analysis results in the following equation for laminar flame
speed:
2 ! 1=2
0 E=RT b
2k Z e RT b
u [ ¼ (15.7)
c p r c u ðT b T u Þ E
u