Page 169 - Advances in Biomechanics and Tissue Regeneration

8.5 PATIENT-SPECIFIC CARDIAC PODI COMPUTATION 165

TABLE 8.4 Dimensions of the Biventricle Model
Values
Range Choice References
LEFT VENTRICLE
Volume (mL) 22–48 36.98 [38, 40]
Base diameter, ⌀ LV (cm) 2.2–4.0 3.1 [41, 91]
Wall thickness, t LV (cm) 1.09–1.45 1.27 [92]
Diameter-depth ratio 2–3 2.37 [40]
endo
Endocardium height, h LV (cm) – 7.35 –
epi
Epicardium height, h LV (cm) – 8.62 –
RIGHT VENTRICLE
Volume (mL) 24–62 51.21 [38, 40]
Base diameter, l RV (cm) 1.2–2.6 1.9 [39]
Wall thickness, t RV (cm) 3.5–8.5 0.63 [93]
endo
Endocardium height, h RV (cm) – 7.00 –
epi
Epicardium height, h RV (cm) – 8.20 –

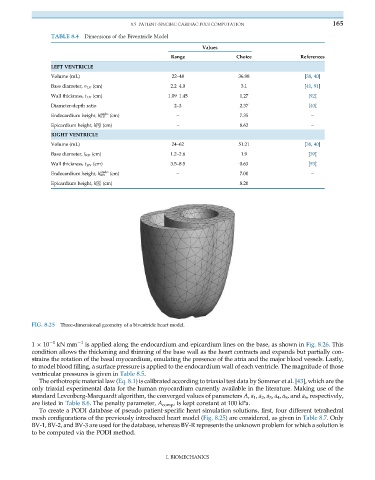
FIG. 8.25 Three-dimensional geometry of a biventricle heart model.

1 10 1 kN mm 1 is applied along the endocardium and epicardium lines on the base, as shown in Fig. 8.26. This
condition allows the thickening and thinning of the base wall as the heart contracts and expands but partially con-
strains the rotation of the basal myocardium, emulating the presence of the atria and the major blood vessels. Lastly,
to model blood filling, a surface pressure is applied to the endocardium wall of each ventricle. The magnitude of those
ventricular pressures is given in Table 8.5.
The orthotropic material law (Eq. 8.1) is calibrated according to triaxial test data by Sommer et al. [43], which are the
only triaxial experimental data for the human myocardium currently available in the literature. Making use of the
standard Levenberg-Marquardt algorithm, the converged values of parameters A, a 1 , a 2 , a 3 , a 4 , a 5 , and a 6 , respectively,
are listed in Table 8.6. The penalty parameter, A comp , is kept constant at 100 kPa.
To create a PODI database of pseudo patient-specific heart simulation solutions, first, four different tetrahedral
mesh configurations of the previously introduced heart model (Fig. 8.25) are considered, as given in Table 8.7. Only
BV-1, BV-2, and BV-3 are used for the database, whereas BV-R represents the unknown problem for which a solution is
to be computed via the PODI method.

I. BIOMECHANICS