Page 174 - Advances in Biomechanics and Tissue Regeneration

170 8. TOWARDS THE REAL-TIME MODELING OF THE HEART

Calculation time
600

500
Time taken (s) 400

300

200
200 300 400 500 600 700 800 900 1000
Nodes
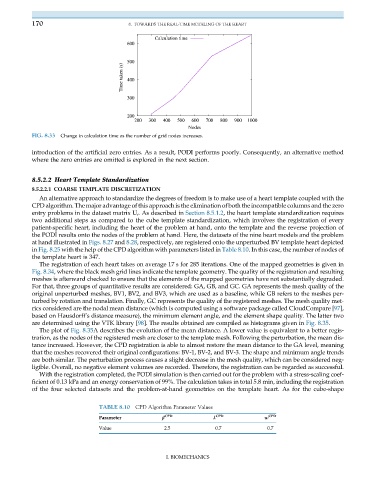
FIG. 8.33 Change in calculation time as the number of grid nodes increases.

introduction of the artificial zero entries. As a result, PODI performs poorly. Consequently, an alternative method
where the zero entries are omitted is explored in the next section.

8.5.2.2 Heart Template Standardization
8.5.2.2.1 COARSE TEMPLATE DISCRETIZATION
An alternative approach to standardize the degrees of freedom is to make use of a heart template coupled with the
CPD algorithm. The major advantage of this approach is the elimination of both the incompatible columns and the zero
entry problems in the dataset matrix U i . As described in Section 8.5.1.2, the heart template standardization requires
two additional steps as compared to the cube template standardization, which involves the registration of every
patient-specific heart, including the heart of the problem at hand, onto the template and the reverse projection of
the PODI results onto the nodes of the problem at hand. Here, the datasets of the nine heart models and the problem
at hand illustrated in Figs. 8.27 and 8.28, respectively, are registered onto the unperturbed BV template heart depicted
in Fig. 8.25 with the help of the CPD algorithm with parameters listed in Table 8.10. In this case, the number of nodes of
the template heart is 347.
The registration of each heart takes on average 17 s for 285 iterations. One of the mapped geometries is given in
Fig. 8.34, where the black mesh grid lines indicate the template geometry. The quality of the registration and resulting
meshes is afterward checked to ensure that the elements of the mapped geometries have not substantially degraded.
For that, three groups of quantitative results are considered: GA, GB, and GC. GA represents the mesh quality of the
original unperturbed meshes, BV1, BV2, and BV3, which are used as a baseline, while GB refers to the meshes per-
turbed by rotation and translation. Finally, GC represents the quality of the registered meshes. The mesh quality met-
rics considered are the nodal mean distance (which is computed using a software package called CloudCompare [97],
based on Hausdorff’s distance measure), the minimum element angle, and the element shape quality. The latter two
are determined using the VTK library [98]. The results obtained are compiled as histograms given in Fig. 8.35.
The plot of Fig. 8.35A describes the evolution of the mean distance. A lower value is equivalent to a better regis-
tration, as the nodes of the registered mesh are closer to the template mesh. Following the perturbation, the mean dis-
tance increased. However, the CPD registration is able to almost restore the mean distance to the GA level, meaning
that the meshes recovered their original configurations: BV-1, BV-2, and BV-3. The shape and minimum angle trends
are both similar. The perturbation process causes a slight decrease in the mesh quality, which can be considered neg-
ligible. Overall, no negative element volumes are recorded. Therefore, the registration can be regarded as successful.
With the registration completed, the PODI simulation is then carried out for the problem with a stress-scaling coef-
ficient of 0.13 kPa and an energy conservation of 99%. The calculation takes in total 5.8 min, including the registration
of the four selected datasets and the problem-at-hand geometries on the template heart. As for the cube-shape

TABLE 8.10 CPD Algorithm Parameter Values
Parameter β CPD λ CPD w CPD

Value 2.5 0.7 0.7

I. BIOMECHANICS