Page 172 - Advances in Biomechanics and Tissue Regeneration

168 8. TOWARDS THE REAL-TIME MODELING OF THE HEART

Displacement
1.59e+01

11.91

7.94
3.97

2.20e-05

(A)

Displacement
1.59e+01
11.925
7.95
3.975
2.20e-05
(B) (C)
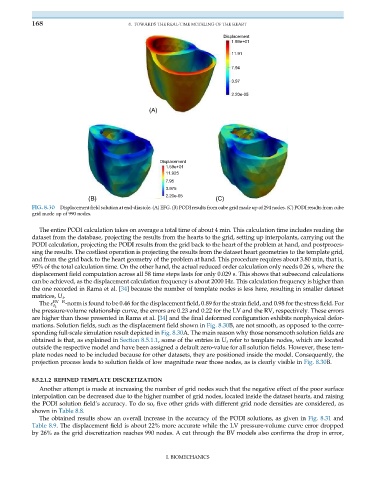
FIG. 8.30 Displacement field solution at end-diastole. (A) EFG. (B) PODI results from cube grid made up of 294 nodes. (C) PODI results from cube
grid made up of 990 nodes.

The entire PODI calculation takes on average a total time of about 4 min. This calculation time includes reading the
dataset from the database, projecting the results from the hearts to the grid, setting up interpolants, carrying out the
PODI calculation, projecting the PODI results from the grid back to the heart of the problem at hand, and postproces-
sing the results. The costliest operation is projecting the results from the dataset heart geometries to the template grid,
and from the grid back to the heart geometry of the problem at hand. This procedure requires about 3.80 min, that is,
95% of the total calculation time. On the other hand, the actual reduced order calculation only needs 0.26 s, where the
displacement field computation across all 58 time steps lasts for only 0.029 s. This shows that subsecond calculations
can be achieved, as the displacement calculation frequency is about 2000 Hz. This calculation frequency is higher than
the one recorded in Rama et al. [34] because the number of template nodes is less here, resulting in smaller dataset
matrices, U i .
The ε BV R -norm is found to be 0.46 for the displacement field, 0.89 for the strain field, and 0.98 for the stress field. For
‘ 2
the pressure-volume relationship curve, the errors are 0.23 and 0.22 for the LV and the RV, respectively. These errors
are higher than those presented in Rama et al. [34] and the final deformed configuration exhibits nonphysical defor-
mations. Solution fields, such as the displacement field shown in Fig. 8.30B, are not smooth, as opposed to the corre-
sponding full-scale simulation result depicted in Fig. 8.30A. The main reason why those nonsmooth solution fields are
obtained is that, as explained in Section 8.5.1.1, some of the entries in U i refer to template nodes, which are located
outside the respective model and have been assigned a default zero-value for all solution fields. However, these tem-
plate nodes need to be included because for other datasets, they are positioned inside the model. Consequently, the
projection process leads to solution fields of low magnitude near those nodes, as is clearly visible in Fig. 8.30B.

8.5.2.1.2 REFINED TEMPLATE DISCRETIZATION
Another attempt is made at increasing the number of grid nodes such that the negative effect of the poor surface
interpolation can be decreased due to the higher number of grid nodes, located inside the dataset hearts, and raising
the PODI solution field’s accuracy. To do so, five other grids with different grid node densities are considered, as
shown in Table 8.8.
The obtained results show an overall increase in the accuracy of the PODI solutions, as given in Fig. 8.31 and
Table 8.9. The displacement field is about 22% more accurate while the LV pressure-volume curve error dropped
by 26% as the grid discretization reaches 990 nodes. A cut through the BV models also confirms the drop in error,

I. BIOMECHANICS