Page 191 - Advances in Biomechanics and Tissue Regeneration

9.3 EQUILIBRIUM APPLICATIONS: BOUNDARY CONDITIONS AND LOADING 187

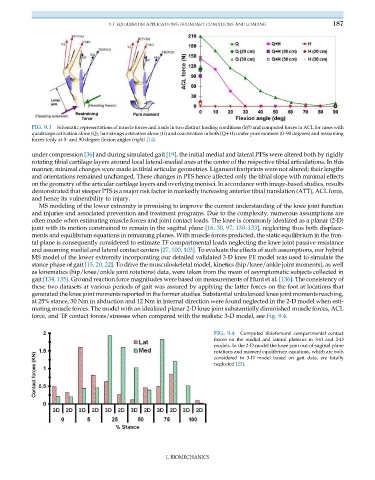
FIG. 9.3 Schematic representations of muscle forces and loads in two distinct loading conditions (left) and computed forces in ACL for cases with
quadriceps activation alone (Q), hamstrings activation alone (H) and coactivation in both (Q+H) under pure moment (0–90 degrees) and restraining
forces (only at 0- and 90-degree flexion angles (right) [14].

under compression [36] and during simulated gait [19], the initial medial and lateral PTSs were altered both by rigidly
rotating tibial cartilage layers around local lateral-medial axes at the center of the respective tibial articulations. In this
manner, minimal changes were made in tibial articular geometries. Ligament footprints were not altered; their lengths
and orientations remained unchanged. These changes in PTS hence affected only the tibial slope with minimal effects
on the geometry of the articular cartilage layers and overlying menisci. In accordance with image-based studies, results
demonstrated that steeper PTS is a major risk factor in markedly increasing anterior tibial translation (ATT), ACL force,
and hence its vulnerability to injury.
MS modeling of the lower extremity is promising to improve the current understanding of the knee joint function
and injuries and associated prevention and treatment programs. Due to the complexity, numerous assumptions are
often made when estimating muscle forces and joint contact loads. The knee is commonly idealized as a planar (2-D)
joint with its motion constrained to remain in the sagittal plane [16, 30, 97, 130–133], neglecting thus both displace-
ments and equilibrium equations in remaining planes. With muscle forces predicted, the static equilibrium in the fron-
tal plane is consequently considered to estimate TF compartmental loads neglecting the knee joint passive resistance
and assuming medial and lateral contact centers [27, 100, 103]. To evaluate the effects of such assumptions, our hybrid
MS model of the lower extremity incorporating our detailed validated 3-D knee FE model was used to simulate the
stance phase of gait [15, 20, 22]. To drive the musculoskeletal model, kinetics (hip/knee/ankle joint moments), as well
as kinematics (hip/knee/ankle joint rotations) data, were taken from the mean of asymptomatic subjects collected in
gait [134, 135]. Ground reaction force magnitudes were based on measurements of Hunt et al. [136]. The consistency of
these two datasets at various periods of gait was assured by applying the latter forces on the foot at locations that
generated the knee joint moments reported in the former studies. Substantial unbalanced knee joint moments reaching,
at 25% stance, 30 Nm in abduction and 12 Nm in internal direction were found neglected in the 2-D model when esti-
mating muscle forces. The model with an idealized planar 2-D knee joint substantially diminished muscle forces, ACL
force, and TF contact forces/stresses when compared with the realistic 3-D model, see Fig. 9.4.

FIG. 9.4 Computed tibiofemoral compartmental contact
forces on the medial and lateral plateaus in 3-D and 2-D
models. In the 2-D model the knee joint out-of-sagittal plane
rotations and moment equilibrium equations, which are both
considered in 3-D model based on gait data, are totally
neglected [23].

I. BIOMECHANICS