Page 130 - Advances in Renewable Energies and Power Technologies

6. Forecasting Methods for Different Forecast Horizons 103

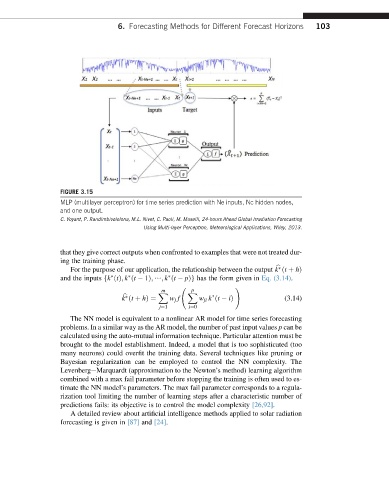
FIGURE 3.15
MLP (multilayer perceptron) for time series prediction with Ne inputs, Nc hidden nodes,
and one output.
C. Voyant, P. Randimbivololona, M.L. Nivet, C. Paoli, M. Muselli, 24-hours Ahead Global Irradiation Forecasting
Using Multi-layer Perceptron, Meteorological Applications, Wiley, 2013.

that they give correct outputs when confronted to examples that were not treated dur-
ing the training phase.
b
For the purpose of our application, the relationship between the output k ðt þ hÞ

and the inputs fk ðtÞ; k ðt 1Þ; /; k ðt pÞg has the form given in Eq. (3.14).
!
m p
X X

b
k ðt þ hÞ¼ w j f w ji k ðt iÞ (3.14)
j¼1 i¼0
The NN model is equivalent to a nonlinear AR model for time series forecasting
problems. In a similar way as the AR model, the number of past input values p can be
calculated using the auto-mutual information technique. Particular attention must be
brought to the model establishment. Indeed, a model that is too sophisticated (too
many neurons) could overfit the training data. Several techniques like pruning or
Bayesian regularization can be employed to control the NN complexity. The
LevenbergeMarquardt (approximation to the Newton’s method) learning algorithm
combined with a max fail parameter before stopping the training is often used to es-
timate the NN model’s parameters. The max fail parameter corresponds to a regula-
rization tool limiting the number of learning steps after a characteristic number of
predictions fails: its objective is to control the model complexity [26,92].
A detailed review about artificial intelligence methods applied to solar radiation
forecasting is given in [87] and [24].