Page 51 - Aerodynamics for Engineering Students

34 Aerodynamics for Engineering Students

Again making the approximations that cosa N 1 and CD sina can be ignored, the
Eqn (1.54), above, becomes

(1.55)

At first sight this would suggest that kCp is always less than XAC/C. However, CM, is
almost invariably negative, so that in fact kcp is numerically greater than XAC/C and
the centre of pressure is behind the aerodynamic centre.

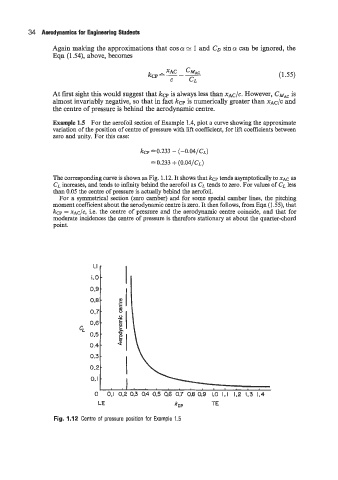
Example 1.5 For the aerofoil section of Example 1.4, plot a curve showing the approximate
variation of the position of centre of pressure with lift coefficient, for lift coefficients between
zero and unity. For this case:

kcp 0.233 - (-0.04/C~)
fi 0.233 + (0.04/C~)

The corresponding curve is shown as Fig. 1.12. It shows that kcp tends asymptotically to XAC as
CL increases, and tends to infinity behind the aerofoil as CL tends to zero. For values of CL less
than 0.05 the centre of pressure is actually behind the aerofoil.
For a symmetrical section (zero camber) and for some special camber lines, the pitching
moment coefficient about the aerodynamic centre is zero. It then follows, from Eqn (1.55), that
kcp = XAC/C, i.e. the centre of pressure and the aerodynamic centre coincide, and that for
moderate incidences the centre of pressure is therefore stationary at about the quarter-chord
point.

LE kCP TE

Fig. 1.12 Centre of pressure position for Example 1.5