Page 357 - Air pollution and greenhouse gases from basic concepts to engineering applications for air emission control

11.3 Gaussian-Plume Dispersion Models 335

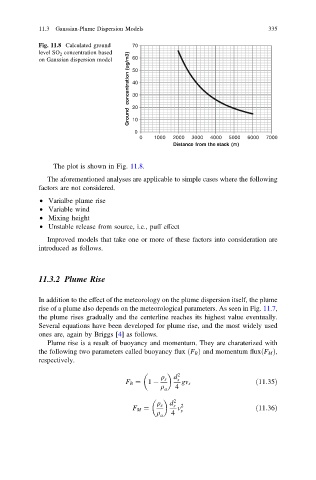
Fig. 11.8 Calculated ground 70
level SO 2 concentration based
Ground concentration (ug/m3) 40
on Gaussian dispersion model 60
50

30
20
10
0
0 1000 2000 3000 4000 5000 6000 7000
Distance from the stack (m)

The plot is shown in Fig. 11.8.

The aforementioned analyses are applicable to simple cases where the following
factors are not considered.
• Varialbe plume rise
• Variable wind
• Mixing height
• Unstable release from source, i.e., puff effect
Improved models that take one or more of these factors into consideration are
introduced as follows.

11.3.2 Plume Rise

In addition to the effect of the meteorology on the plume dispersion itself, the plume
rise of a plume also depends on the meteorological parameters. As seen in Fig. 11.7,
the plume rises gradually and the centerline reaches its highest value eventually.
Several equations have been developed for plume rise, and the most widely used
ones are, again by Briggs [4] as follows.
Plume rise is a result of buoyancy and momentum. They are charaterized with
the following two parameters called buoyancy flux ðF B Þ and momentum fluxðF M Þ,
respectively.

q d
2
F B ¼ 1 s s gv s ð11:35Þ
q a 4
q s d s 2
2
F M ¼ v s ð11:36Þ
q a 4