Page 257 -

SOLVING A MINIMIZATION PROBLEM 237

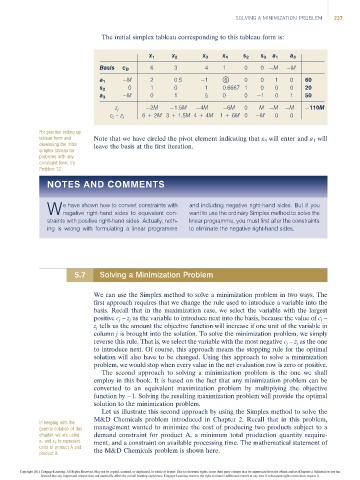
The initial simplex tableau corresponding to this tableau form is:

x 1 x 2 x 3 x 4 s 2 s 3 a 1 a 3
Basis c B 6 3 4 1 0 0 M M

a 1 M 2 0.5 1 *6 0 0 1 0 60
s 2 0 1 0 1 0.6667 1 0 0 0 20
a 3 M 0 1 5 0 0 1 0 1 50
2M 1.5M 4M 6M 0 M M M 110M
z j
6+ 2M 3 + 1.5M 4+4M 1+6M 0 M 0 0
c j – z j
For practise setting up
tableau form and Note that we have circled the pivot element indicating that x 4 will enter and a 1 will
developing the initial leave the basis at the first iteration.
simplex tableau for
problems with any
constraint form, try
Problem 12.

NOTES AND COMMENTS

e have shown how to convert constraints with and including negative right-hand sides. But if you
W negative right-hand sides to equivalent con- want to use the ordinary Simplex method to solve the
straints with positive right-hand sides. Actually, noth- linear programme, you must first alter the constraints
ing is wrong with formulating a linear programme to eliminate the negative right-hand sides.

5.7 Solving a Minimization Problem

We can use the Simplex method to solve a minimization problem in two ways. The
first approach requires that we change the rule used to introduce a variable into the
basis. Recall that in the maximization case, we select the variable with the largest
positive c j – z j as the variable to introduce next into the basis, because the value of c j –
z j tells us the amount the objective function will increase if one unit of the variable in
column j is brought into the solution. To solve the minimization problem, we simply
reverse this rule. That is, we select the variable with the most negative c j – z j as the one
to introduce next. Of course, this approach means the stopping rule for the optimal
solution will also have to be changed. Using this approach to solve a minimization
problem, we would stop when every value in the net evaluation row is zero or positive.
The second approach to solving a minimization problem is the one we shall
employ in this book. It is based on the fact that any minimization problem can be
converted to an equivalent maximization problem by multiplying the objective
function by 1. Solving the resulting maximization problem will provide the optimal
solution to the minimization problem.
Let us illustrate this second approach by using the Simplex method to solve the
M&D Chemicals problem introduced in Chapter 2. Recall that in this problem,
In keeping with the
general notation of this management wanted to minimize the cost of producing two products subject to a
chapter, we are using demand constraint for product A, a minimum total production quantity require-
x 1 and x 2 to represent ment, and a constraint on available processing time. The mathematical statement of
units of product A and
product B. the M&D Chemicals problem is shown here.

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.