Page 260 -

240 CHAPTER 5 LINEAR PROGRAMMING: THE SIMPLEX METHOD

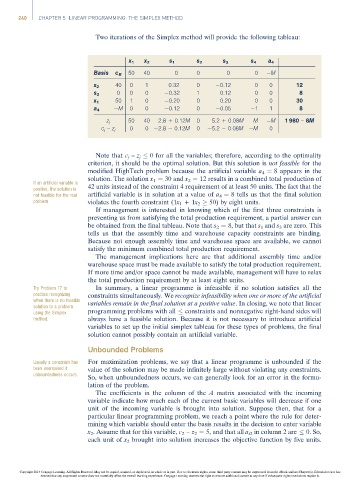
Two iterations of the Simplex method will provide the following tableau:

x 1 x 2 s 1 s 2 s 3 s 4 a 4
Basis c B 50 40 0 0 0 0 M

x 2 40 0 1 0.32 0 0.12 0 0 12
s 2 0 0 0 0.32 1 0.12 0 0 8
x 1 50 1 0 0.20 0 0.20 0 0 30
a 4 M 0 0 0.12 0 0.05 1 1 8
50 40 2.8 + 0.12M 0 5.2 + 0.08M M M 1 980 – 8M
z j
0 0 2.8 0.12M 0 5.2 0.08M M 0
c j – z j

Note that c j – z j 0 for all the variables; therefore, according to the optimality
criterion, it should be the optimal solution. But this solution is not feasible for the
modified HighTech problem because the artificial variable a 4 ¼ 8 appears in the
solution. The solution x 1 ¼ 30 and x 2 ¼ 12 results in a combined total production of
If an artificial variable is
positive, the solution is 42 units instead of the constraint 4 requirement of at least 50 units. The fact that the
not feasible for the real artificial variable is in solution at a value of a 4 ¼ 8 tells us that the final solution
problem. violates the fourth constraint (1x 1 +1x 2 50) by eight units.
If management is interested in knowing which of the first three constraints is
preventing us from satisfying the total production requirement, a partial answer can
be obtained from the final tableau. Note that s 2 ¼ 8, but that s 1 and s 3 are zero. This
tells us that the assembly time and warehouse capacity constraints are binding.
Because not enough assembly time and warehouse space are available, we cannot
satisfy the minimum combined total production requirement.
The management implications here are that additional assembly time and/or
warehouse space must be made available to satisfy the total production requirement.
If more time and/or space cannot be made available, management will have to relax
the total production requirement by at least eight units.
Try Problem 17 to In summary, a linear programme is infeasible if no solution satisfies all the
practise recognizing constraints simultaneously. We recognize infeasibility when one or more of the artificial
when there is no feasible variables remain in the final solution at a positive value. In closing, we note that linear
solution to a problem
using the Simplex programming problems with all constraints and nonnegative right-hand sides will
method. always have a feasible solution. Because it is not necessary to introduce artificial
variables to set up the initial simplex tableau for these types of problems, the final
solution cannot possibly contain an artificial variable.

Unbounded Problems
Usually a constraint has For maximization problems, we say that a linear programme is unbounded if the
been overlooked if value of the solution may be made infinitely large without violating any constraints.
unboundedness occurs.
So, when unboundedness occurs, we can generally look for an error in the formu-
lation of the problem.
The coefficients in the column of the A matrix associated with the incoming
variable indicate how much each of the current basic variables will decrease if one
unit of the incoming variable is brought into solution. Suppose then, that for a
particular linear programming problem, we reach a point where the rule for deter-
mining which variable should enter the basis results in the decision to enter variable
x 2 . Assume that for this variable, c 2 – z 2 ¼ 5, and that all a i2 in column 2 are 0. So,
each unit of x 2 brought into solution increases the objective function by five units.

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.