Page 262 -

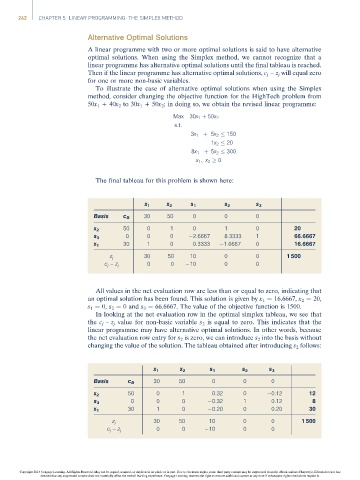
242 CHAPTER 5 LINEAR PROGRAMMING: THE SIMPLEX METHOD

Alternative Optimal Solutions
A linear programme with two or more optimal solutions is said to have alternative
optimal solutions. When using the Simplex method, we cannot recognize that a
linear programme has alternative optimal solutions until the final tableau is reached.
Then if the linear programme has alternative optimal solutions, c j – z j will equal zero
for one or more non-basic variables.
To illustrate the case of alternative optimal solutions when using the Simplex
method, consider changing the objective function for the HighTech problem from
50x 1 +40x 2 to 30x 1 +50x 2 ; in doing so, we obtain the revised linear programme:
Max 30x 1 þ 50x 2
s:t:
3x 1 þ 5x 2 150
1x 2 20
8x 1 þ 5x 2 300
x 1 ; x 2 0

The final tableau for this problem is shown here:

x 1 x 2 s 1 s 2 s 3
Basis c B 30 50 0 0 0

x 2 50 0 1 0 1 0 20
s 3 0 0 0 2.6667 8.3333 1 66.6667
x 1 30 1 0 0.3333 1.6667 0 16.6667
30 50 10 0 0 1 500
z j
0 0 10 0 0
c j – z j

All values in the net evaluation row are less than or equal to zero, indicating that
an optimal solution has been found. This solution is given by x 1 ¼ 16.6667, x 2 ¼ 20,
s 1 ¼ 0, s 2 ¼ 0 and s 3 ¼ 66.6667. The value of the objective function is 1500.
In looking at the net evaluation row in the optimal simplex tableau, we see that
the c j – z j value for non-basic variable s 2 is equal to zero. This indicates that the
linear programme may have alternative optimal solutions. In other words, because
the net evaluation row entry for s 2 is zero, we can introduce s 2 into the basis without
changing the value of the solution. The tableau obtained after introducing s 2 follows:

x 1 x 2 s 1 s 2 s 3
Basis c B 30 50 0 0 0
50 0 1 0.32 0 0.12 12
x 2
0 0 0 0.32 1 0.12 8
s 3
30 1 0 0.20 0 0.20 30
x 1
z j 30 50 10 0 0 1 500
c j – z j 0 0 10 0 0

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.