Page 620 -

600 CHAPTER 14 MULTICRITERIA DECISIONS

Let us now continue the graphical solution procedure. The goal equation for the
priority level 2 goal is:
þ

3U þ 5H d þ d ¼ 9000
2 2
þ

When both d and d equal zero, this equation reduces to 3U +5H ¼ 9000; we
2 2
show the graph with this equation in Figure 14.3.
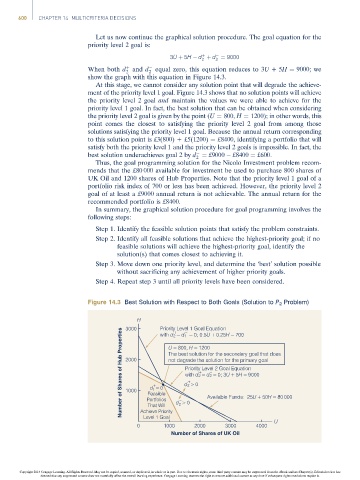
At this stage, we cannot consider any solution point that will degrade the achieve-
ment of the priority level 1 goal. Figure 14.3 shows that no solution points will achieve
the priority level 2 goal and maintain the values we were able to achieve for the
priority level 1 goal. In fact, the best solution that can be obtained when considering
the priority level 2 goal is given by the point (U ¼ 800, H ¼ 1200); in other words, this
point comes the closest to satisfying the priority level 2 goal from among those
solutions satisfying the priority level 1 goal. Because the annual return corresponding
to this solution point is £3(800) + £5(1200) ¼ £8400, identifying a portfolio that will
satisfy both the priority level 1 and the priority level 2 goals is impossible. In fact, the

best solution underachieves goal 2 by d ¼ £9000 £8400 ¼ £600:
2
Thus, the goal programming solution for the Nicolo Investment problem recom-
mends that the £80 000 available for investment be used to purchase 800 shares of
UK Oil and 1200 shares of Hub Properties. Note that the priority level 1 goal of a
portfolio risk index of 700 or less has been achieved. However, the priority level 2
goal of at least a £9000 annual return is not achievable. The annual return for the
recommended portfolio is £8400.
In summary, the graphical solution procedure for goal programming involves the
following steps:

Step 1. Identify the feasible solution points that satisfy the problem constraints.
Step 2. Identify all feasible solutions that achieve the highest-priority goal; if no
feasible solutions will achieve the highest-priority goal, identify the
solution(s) that comes closest to achieving it.
Step 3. Move down one priority level, and determine the ‘best’ solution possible
without sacrificing any achievement of higher priority goals.
Step 4. Repeat step 3 until all priority levels have been considered.

Figure 14.3 Best Solution with Respect to Both Goals (Solution to P 2 Problem)

H Priority Level 1 Goal Equation
3000
Number of Shares of Hub Properties 2000 Feasible U = 800, H = 1200 Available Funds: 25U + 50H = 80 000
+
–
with d 2 = d 1 = 0; 0.5U + 0.25H = 700
The best solution for the secondary goal that does
not degrade the solution for the primary goal
Priority Level 2 Goal Equation
+
–
with d 2 = d 2 = 0; 3U + 5H = 9000
+
d 2 > 0
+
d = 0
1
1000
Portfolios
–
d > 0
2
That Will
Achieve Priority
Level 1 Goal
U
0 1000 2000 3000 4000
Number of Shares of UK Oil
Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.