Page 69 -

GRAPHICAL SOLUTION PROCEDURE 49

on the line is not always as easy as shown in the GulfGolf problem. For example,
suppose a company manufactures two models of a small handheld computer: the
Assistant (A) and the Professional (P). Management needs 50 units of the Professio-
nal model for its own salesforce, and expects sales of the Professional to be at most
one-half of the sales of the Assistant. A constraint enforcing this requirement is:
P 50 0:5A
or
2P 100 A
or

2P A 100
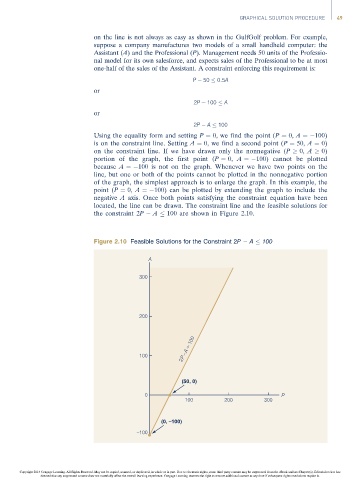
Using the equality form and setting P ¼ 0, we find the point (P ¼ 0, A ¼ 100)
is on the constraint line. Setting A ¼ 0, we find a second point (P ¼ 50, A ¼ 0)
on the constraint line. If we have drawn only the nonnegative (P 0, A 0)
portion of the graph, the first point (P ¼ 0, A ¼ 100) cannot be plotted
because A ¼ 100 is not on the graph. Whenever we have two points on the
line, but one or both of the points cannot be plotted in the nonnegative portion
of the graph, the simplest approach is to enlarge the graph. In this example, the
point (P ¼ 0, A ¼ 100) can be plotted by extending the graph to include the
negative A axis. Once both points satisfying the constraint equation have been
located, the line can be drawn. The constraint line and the feasible solutions for
the constraint 2P A 100 are shown in Figure 2.10.

Figure 2.10 Feasible Solutions for the Constraint 2P A 100

A

300

200

2 P – A = 100

100

(50, 0)
0 P
100 200 300

(0, –100)
–100

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.