Page 47 - Analog and Digital Filter Design

44 Analog and Digital Filter Design

Frequency

Freqency
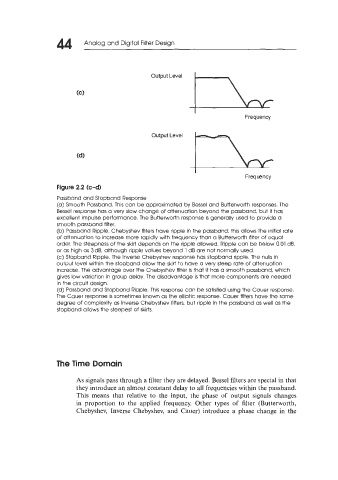
Figure 2.2 (c-d)
Passband and Stopband Response
(a) Smooth Passband. This can be approximated by Bessel and Butterworth responses. The
Bessel response has a very slow change of attenuation beyond the passband, but it has
excellent impulse performance. The Butterworth response is generally used to provide a
smooth passband filter.
(b) Passband Ripple. Chebyshev filters have ripple in the passband; this allows the initial rate
of attenuation to increase more rapidly with frequency than a Butterworth filter of equal
order. The steepness of the skirt depends on the ripple allowed. Ripple can be below 0.01 dB,
or as high as 3dB, although ripple values beyond 1 dB are not normally used.
(c) Stopband Ripple. The Inverse Chebyshev response has stopband ripple. The nulls in
output level within the stopband allow the skirt to have a very steep rate of attenuation
increase. The advantage over the Chebyshev filter is that it has a smooth passband, which
gives low variation in group delay. The disadvantage is that more components are needed
in the circuit design.
(d) Passband and Stopband Ripple. This response can be satisfied using the Cauer response.
The Cauer response is sometimes known as the elliptic response. Cauer filters have the same
degree of complexity as Inverse Chebyshev filters, but ripple in the passband as well as the
stopband allows the steepest of skirts.

The Time Domain

As signals pass through a filter they are delayed. Bessel filters are special in that
they introduce an almost constant delay to all frequencies within the passband.
This means that relative to the input, the phase of output signals changes
in proportion to the applied frequency. Other types of filter (Butterworth,
Chebyshev, Inverse Chebyshev, and Cauer) introduce a phase change in the