Page 274 - Analysis and Design of Energy Geostructures

Thermohydromechanical behaviour of soils and soil structure interfaces 249

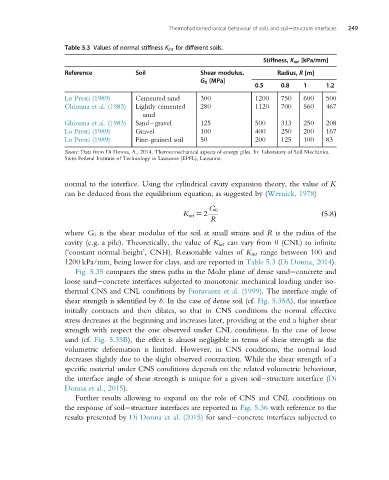
Table 5.3 Values of normal stiffness K int for different soils.
Stiffness, K int [kPa/mm]
Reference Soil Shear modulus, Radius, R [m]
G 0 [MPa]
0.5 0.8 1 1.2
Lo Presti (1989) Cemented sand 300 1200 750 600 500
Ghionna et al. (1983) Lightly cemented 280 1120 700 560 467
sand
Ghionna et al. (1983) Sand gravel 125 500 313 250 208
Lo Presti (1989) Gravel 100 400 250 200 167
Lo Presti (1989) Fine-grained soil 50 200 125 100 83
Source: Data from Di Donna, A., 2014. Thermomechanical aspects of energy piles. In: Laboratory of Soil Mechanics.
Swiss Federal Institute of Technology in Lausanne (EPFL), Lausanne.

normal to the interface. Using the cylindrical cavity expansion theory, the value of K
can be deduced from the equilibrium equation, as suggested by (Wernick, 1978)

G 0
K int 5 2 ð5:8Þ
R
where G 0 is the shear modulus of the soil at small strains and R is the radius of the
cavity (e.g. a pile). Theoretically, the value of K int can vary from 0 (CNL) to infinite
(‘constant normal height’, CNH). Reasonable values of K int range between 100 and
1200 kPa/mm, being lower for clays, and are reported in Table 5.3 (Di Donna, 2014).
Fig. 5.35 compares the stress paths in the Mohr plane of dense sand concrete and
loose sand concrete interfaces subjected to monotonic mechanical loading under iso-
thermal CNS and CNL conditions by Fioravante et al. (1999). The interface angle of
shear strength is identified by δ. In the case of dense soil (cf. Fig. 5.35A), the interface
initially contracts and then dilates, so that in CNS conditions the normal effective
stress decreases at the beginning and increases later, providing at the end a higher shear
strength with respect the one observed under CNL conditions. In the case of loose
sand (cf. Fig. 5.35B), the effect is almost negligible in terms of shear strength as the
volumetric deformation is limited. However, in CNS conditions, the normal load
decreases slightly due to the slight observed contraction. While the shear strength of a
specific material under CNS conditions depends on the related volumetric behaviour,
the interface angle of shear strength is unique for a given soil structure interface (Di
Donna et al., 2015).
Further results allowing to expand on the role of CNS and CNL conditions on
the response of soil structure interfaces are reported in Fig. 5.36 with reference to the
results presented by Di Donna et al. (2015) for sand concrete interfaces subjected to