Page 360 - Applied Numerical Methods Using MATLAB

CONSTRAINED OPTIMIZATION 349

>> nm722
xo_Nelder = 1.2118 0.5765 xo_steep = 1.2768 0.5989
fo_Nelder = 0.5322 %min value fo_steep = 0.2899 %not a minimum
co_Nelder = -1.2118 co_steep = -1.2768
-0.5765 -0.5989
-1.7573 %high margin -1.5386
-0.0000 %no margin 0.1525 %violating
-0.0000 %no margin -0.0001
xo_s = 1.2118 0.5765 Warning: .. Gradient must be provided
fo_s = 0.5322 %min value ........
Maximum # of function evaluations
exceeded;
xo_u = 1.2843 0.6015
fo_u = 0.2696 %not a minium

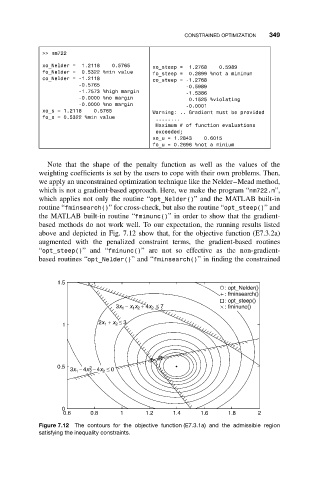
Note that the shape of the penalty function as well as the values of the
weighting coefficients is set by the users to cope with their own problems. Then,
we apply an unconstrained optimization technique like the Nelder–Mead method,
which is not a gradient-based approach. Here, we make the program “nm722.m”,
which applies not only the routine “opt_Nelder()” and the MATLAB built-in
routine “fminsearch()” for cross-check, but also the routine “opt_steep()”and
the MATLAB built-in routine “fminunc()” in order to show that the gradient-
based methods do not work well. To our expectation, the running results listed
above and depicted in Fig. 7.12 show that, for the objective function (E7.3.2a)
augmented with the penalized constraint terms, the gradient-based routines
“opt_steep()”and “fminunc()” are not so effective as the non-gradient-
based routines “opt_Nelder()”and “fminsearch()” in finding the constrained

1.5
: opt_Nelder()
+ : fminsearch()
: opt_steep()
3x 1 − x 1 x 2 + 4x 2 ≤ 7 × : fminunc()

2x 1 + x 2 ≤ 3
1

0.5 2
3x 1 − 4x 2 − 4x 2 ≤ 0

0
0.6 0.8 1 1.2 1.4 1.6 1.8 2
Figure 7.12 The contours for the objective function (E7.3.1a) and the admissible region
satisfying the inequality constraints.