Page 472 - Applied Numerical Methods Using MATLAB

APPENDIX A

MEAN VALUE THEOREM

1
Theorem A.1. Mean Value Theorem . Let a function f(x) be continuous on
the interval [a, b] and differentiable over (a, b). Then, there exists at least one
point ξ between a and b at which
f(b) − f(a)

f (ξ) = , f (b) = f(a) + f (ξ)(b − a) (A.1)
b − a
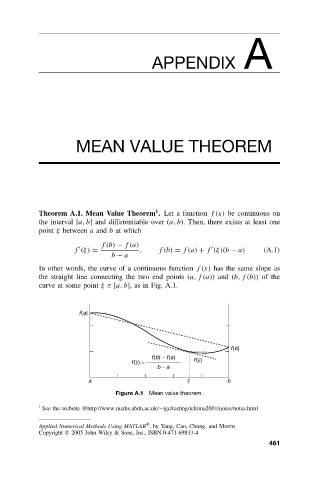
In other words, the curve of a continuous function f(x) has the same slope as
the straight line connecting the two end points (a, f (a))and (b, f (b))of the
curve at some point ξ ∈ [a, b], as in Fig. A.1.

f(a)

f(b)
f(b) − f(a)
f'(x) = f'(x)
b − a
a x b
Figure A.1 Mean value theorem.
1 See the website @http://www.maths.abdn.ac.uk/∼igc/testing/tch/ma2001/notes/notes.html


Applied Numerical Methods Using MATLAB , by Yang, Cao, Chung, and Morris
Copyright  2005 John Wiley & Sons, I nc., ISBN 0-471-69833-4

461