Page 86 - Applied Numerical Methods Using MATLAB

SOLUTION FOR A SYSTEM OF LINEAR EQUATIONS 75

x 2
2 +
x
row
(A)
space
1.5
o+
(3/5, 6/5) = x
(1, 1) = x o
1
solution
space

(3, 0)
x 1
0 1 2 3
o−
x null
space
(A)
x −

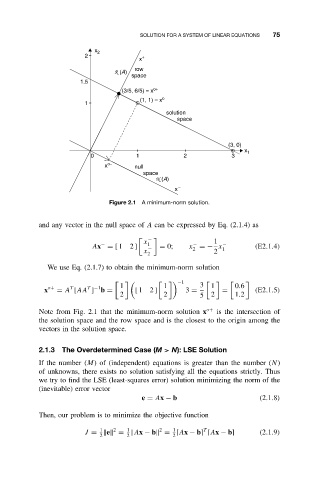
Figure 2.1 A minimum-norm solution.

and any vector in the null space of A can be expressed by Eq. (2.1.4) as

x 1 1
−
−
−
Ax = [ 1 2 ] = 0; x =− x 1 − (E2.1.4)
2
x − 2
2
We use Eq. (2.1.7) to obtain the minimum-norm solution

−1 3 0.6
1
1
1
T −1
T
x o+ = A [AA ] b = [ 12 ] 3 = = (E2.1.5)
2 2 5 2 1.2
Note from Fig. 2.1 that the minimum-norm solution x o+ is the intersection of
the solution space and the row space and is the closest to the origin among the
vectors in the solution space.
2.1.3 The Overdetermined Case (M > N): LSE Solution
If the number (M) of (independent) equations is greater than the number (N)
of unknowns, there exists no solution satisfying all the equations strictly. Thus
we try to find the LSE (least-squares error) solution minimizing the norm of the
(inevitable) error vector
e = Ax − b (2.1.8)

Then, our problem is to minimize the objective function
T
1
2
2
1
1
J = ||e|| = ||Ax − b|| = [Ax − b] [Ax − b] (2.1.9)
2 2 2