Page 16 - Applied Petroleum Geomechanics

6 Applied Petroleum Geomechanics

600
Darley Dale sandstone
Darl ey Dal e sandstone
500
400
σ 1 (MPa) σ 1 (MPa) 300 σ 3 3 =110 MPa
σ =110 MPa

200
σ
σ 3 3 =70 MP a
σ =70 MPa
100
σ 3 3 =3 5 MP a
σ =35 MPa
0
0 20 40 60 80 100 120 140
p p pore fluid (MPa)
(MPa)
pore fluid
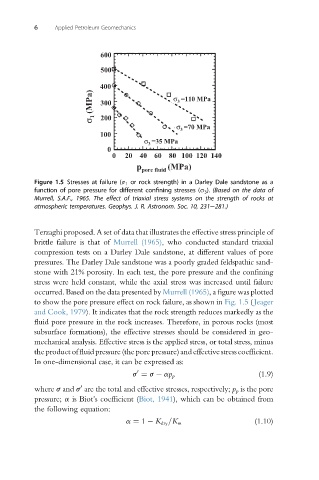
Figure 1.5 Stresses at failure (s 1 or rock strength) in a Darley Dale sandstone as a
function of pore pressure for different confining stresses (s 3 ). (Based on the data of
Murrell, S.A.F., 1965. The effect of triaxial stress systems on the strength of rocks at
atmospheric temperatures. Geophys. J. R. Astronom. Soc. 10, 231e281.)

Terzaghi proposed. A set of data that illustrates the effective stress principle of
brittle failure is that of Murrell (1965), who conducted standard triaxial
compression tests on a Darley Dale sandstone, at different values of pore
pressures. The Darley Dale sandstone was a poorly graded feldspathic sand-
stone with 21% porosity. In each test, the pore pressure and the confining
stress were held constant, while the axial stress was increased until failure
occurred. Based on the data presented by Murrell (1965),a figure was plotted
to show the pore pressure effect on rock failure, as shown in Fig. 1.5 ( Jeager
and Cook, 1979). It indicates that the rock strength reduces markedly as the
fluid pore pressure in the rock increases. Therefore, in porous rocks (most
subsurface formations), the effective stresses should be considered in geo-
mechanical analysis. Effective stress is the applied stress, or total stress, minus
the product of fluid pressure (the pore pressure) and effective stress coefficient.
In one-dimensional case, it can be expressed as:

0
s ¼ s ap p (1.9)
0
where s and s are the total and effective stresses, respectively; p p is the pore
pressure; a is Biot’s coefficient (Biot, 1941), which can be obtained from
the following equation:

a ¼ 1 K dry =K m (1.10)