Page 20 - Applied Petroleum Geomechanics

10 Applied Petroleum Geomechanics

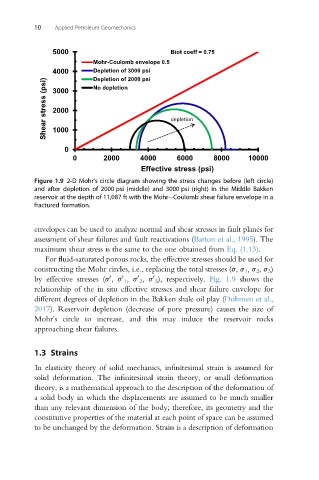
5000 Biot coeff = 0.75
Mohr-Coulomb envelope 0.5
4000 Depletion of 3000 psi
Depletion of 2000 psi
Shear stress (psi) 3000 depleƟon
No depletion

2000

1000

0
0 2000 4000 6000 8000 10000
Effective stress (psi)
Figure 1.9 2-D Mohr’s circle diagram showing the stress changes before (left circle)
and after depletion of 2000 psi (middle) and 3000 psi (right) in the Middle Bakken
reservoir at the depth of 11,087 ft with the MohreCoulomb shear failure envelope in a
fractured formation.

envelopes can be used to analyze normal and shear stresses in fault planes for
assessment of shear failures and fault reactivations (Barton et al., 1995). The
maximum shear stress is the same to the one obtained from Eq. (1.13).
For fluid-saturated porous rocks, the effective stresses should be used for
constructing the Mohr circles, i.e., replacing the total stresses (s, s 1 , s 2 , s 3 )
0
0
0
by effective stresses (s , s 1 , s 2 , s 3 ), respectively. Fig. 1.9 shows the
0
relationship of the in situ effective stresses and shear failure envelope for
different degrees of depletion in the Bakken shale oil play (Dohmen et al.,
2017). Reservoir depletion (decrease of pore pressure) causes the size of
Mohr’s circle to increase, and this may induce the reservoir rocks
approaching shear failures.

1.3 Strains

In elasticity theory of solid mechanics, infinitesimal strain is assumed for
solid deformation. The infinitesimal strain theory, or small deformation
theory, is a mathematical approach to the description of the deformation of
a solid body in which the displacements are assumed to be much smaller
than any relevant dimension of the body; therefore, its geometry and the
constitutive properties of the material at each point of space can be assumed
to be unchanged by the deformation. Strain is a description of deformation