Page 200 - Applied Statistics And Probability For Engineers

c05.qxd 5/13/02 1:50 PM Page 176 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

176 CHAPTER 5 JOINT PROBABILITY DISTRIBUTIONS

If X and Y are independent random variables,

XY XY 0 (5-31)

EXAMPLE 5-31 For the two random variables in Fig. 5-16, show that XY 0.
The two random variables in this example are continuous random variables. In this case
E(XY) is defined as the double integral over the range of (X, Y). That is,
4 2 4 2 4 2
1 2 2 1 2 3
E1XY 2 xy f XY 1x, y2 dx dy 16 £ x y dx§ dy 16 y £ x 3 ` §
0 0 0 0 0 0
4

1 1 4 1
3
2
y 38 34 dy £ y 3 ` § 364 34 32 9
16 6 6
0
0
Also,
4 2 4 2 4 2
1 2 1 3
E1X2 x f XY 1x, y2 dx dy £ x dx§ dy £x 3 ` § dy
16
16
0
0 0 0 0 0
1 4 1
2
£ y 2 ` § 38 34 316 24 4 3
16 0 6
4 2 4 2 4 2
1 2 1 2 2
E1Y 2 y f XY 1x, y2 dx dy y £ x dx§ dy y £ x 2 ` § dy
16
16
0
0 0 0 0 0
2 4 1
3
£ y 3 ` § 364 34 8 3
16 0 8
y
4

3
1
f (x,y) = xy
XY 16
2
1

0 1 2 x
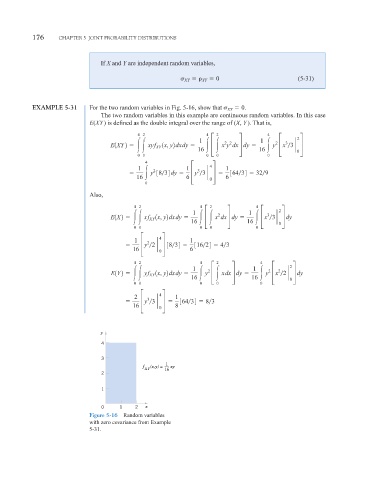
Figure 5-16 Random variables
with zero covariance from Example
5-31.