Page 156 - Applied statistics and probability for engineers

134 Chapter 4/Continuous Random Variables and Probability Distributions

2.0
l
2
0.5
1.6 0.1

1.2
f(x)

0.8 f (x)

0.4

0.0
0 2 4 6 8 10 12 0.1 x
x
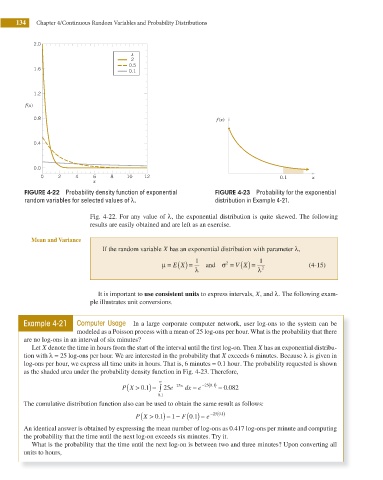
FIGURE 4-22 Probability density function of exponential FIGURE 4-23 Probability for the exponential
random variables for selected values of λ. distribution in Example 4-21.

Fig. 4-22. For any value of λ, the exponential distribution is quite skewed. The following
results are easily obtained and are left as an exercise.
Mean and Variance
If the random variable X has an exponential distribution with parameter λ,
1 1
2
μ = ( ) = and σ = ( ) = (4-15)
V
X
E
X
λ λ 2
It is important to use consistent units to express intervals, X, and λ. The following exam-
ple illustrates unit conversions.

Example 4-21 Computer Usage In a large corporate computer network, user log-ons to the system can be
modeled as a Poisson process with a mean of 25 log-ons per hour. What is the probability that there
are no log-ons in an interval of six minutes?
Let X denote the time in hours from the start of the interval until the i rst log-on. Then X has an exponential distribu-
tion with λ = 25 log-ons per hour. We are interested in the probability that X exceeds 6 minutes. Because λ is given in
log-ons per hour, we express all time units in hours. That is, 6 minutes = 0.1 hour. The probability requested is shown
as the shaded area under the probability density function in Fig. 4-23. Therefore,
25 0 1)
(
. =
.
P X > 0 1) ∫ ∞ 25 e − 25 x dx = e − ( . = 0 082
.
0 1
The cumulative distribution function also can be used to obtain the same result as follows:
P X > 0 1) = − ( . e − ( .
(
25 0 1)
.
F 0 1) =
1
An identical answer is obtained by expressing the mean number of log-ons as 0.417 log-ons per minute and computing
the probability that the time until the next log-on exceeds six minutes. Try it.
What is the probability that the time until the next log-on is between two and three minutes? Upon converting all
units to hours,