Page 72 - Autonomous Mobile Robots

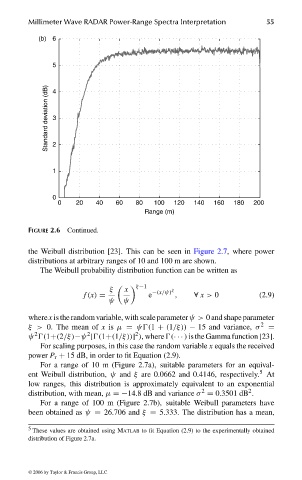
Millimeter Wave RADAR Power-Range Spectra Interpretation 55

(b) 6

5

Standard deviation (dB) 3
4

2

1

0
0 20 40 60 80 100 120 140 160 180 200
Range (m)

FIGURE 2.6 Continued.

the Weibull distribution [23]. This can be seen in Figure 2.7, where power
distributions at arbitrary ranges of 10 and 100 m are shown.
The Weibull probability distribution function can be written as
ξ x
ξ−1 −(x/ψ) ξ
f (x) = e , ∀ x > 0 (2.9)
ψ ψ
wherex istherandomvariable, withscaleparameterψ> 0 andshapeparameter
ξ > 0. The mean of x is µ = ψ (1 + (1/ξ)) − 15 and variance, σ 2 =
2
2
2
ψ (1+(2/ξ)−ψ [ (1+(1/ξ))] ), where (··· )isthe Gamma function [23].
For scaling purposes, in this case the random variable x equals the received
power P r + 15 dB, in order to fit Equation (2.9).
For a range of 10 m (Figure 2.7a), suitable parameters for an equival-
5
ent Weibull distribution, ψ and ξ are 0.0662 and 0.4146, respectively. At
low ranges, this distribution is approximately equivalent to an exponential
2
2
distribution, with mean, µ =−14.8 dB and variance σ = 0.3501 dB .
For a range of 100 m (Figure 2.7b), suitable Weibull parameters have
been obtained as ψ = 26.706 and ξ = 5.333. The distribution has a mean,
5 These values are obtained using Matlab to fit Equation (2.9) to the experimentally obtained
distribution of Figure 2.7a.

© 2006 by Taylor & Francis Group, LLC

FRANKL: “dk6033_c002” — 2006/3/31 — 17:29 — page 55 — #15