Page 185 - Basic physical chemistry for the atmospheric sciences

Gibbs energies, enthalpies, and entropies 1 1 1

t
Appendix V (Con . )
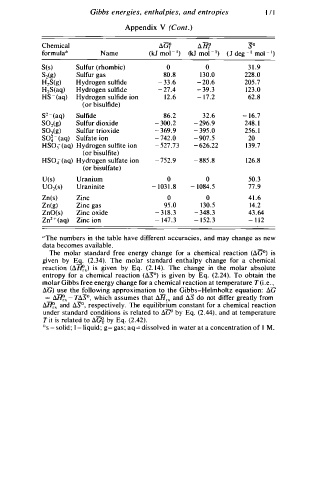
Chemical t1G? t1H? so
formuJa h Name (kJ mo - J 1) (kJ mol - 1 ) ( J deg - 1 mol - 1 )

S(s) Sulfur (rhombic) 0 0 3 1 . 9
S z(g) Sulfur gas 80.8 1 3 0.0 228 .0
d
H2S(g) Hy r ogen sulfide - 3 3 . 6 - 2 0.6 205 .7
H2S(aq) Hydrogen sulfide - 2 7.4 - 39. 3 1 2 3 . 0
HS - (aq) Hydrogen sulfide ion 1 2 . 6 - 1 7 . 2 62.8
(or bisulfide)
s2 - (aq) Sulfide 86 2 32.6 - 1 6.7
.
S02( g) Sulfur dioxide - 3 00.2 - 2 96.9 248. 1
S03(g) Sulfur trioxide - 3 69.9 - 3 95 .0 256. 1
so� - (aq) Sulfate ion - 7 42 .0 - 9 07. 5 20
-
H S 03 ( aq) Hydrogen sulfite ion - 5 27 .73 - 6 26.22 1 3 9.7
(or bisulfite)
-
HS04 ( aq) Hydrogen sulfate ion - 7 52.9 - 885 .8 1 2 6.8
(or bisulfate)
U ( s) Uranium 0 0 50. 3
U02(s) Uraninite - 1 03 1 . 8 - 1 0 84. 5 77 .9
Zn(s) Zinc 0 0 4 1 .6
Zn(g) Zinc gas 95 .0 1 3 0.5 14.2
ZnO(s) Zinc oxide - 3 1 8 . 3 - 3 48. 3 43. 6 4
Zn2 + (aq) Zinc ion - 1 47. 3 - 1 52. 3 - 1 1 2

" T he numbers in the table have different accuracies , and may change as new
data becomes available .
The molar standard free energy change for a chemical reaction (t1G0) is
given by Eq. (2.34). The molar standard enthalpy change for a chemical
reaction (!1-mx) is given by Eq. (2. 14). The change in the molar absolute
entropy for a chemical reaction (t1S0) is given by Eq. (2.24). To obtain the
molar Gibbs free energy change for a chemical reaction at temperature T (i .e . ,
SG) use the following approximation to the Gibbs-Helmholtz equation : t1G
= !1�, - T t1S0, which assumes that t1Hrx and t1S do not differ greatly from
l
t1�x and t1S0, respective y . The equilibrium constant for a chemical reaction
under standard conditions is related to t1G1 by Eq. (2 .44) , and at temperature
T i t is related to t1G} by Eq. (2.42).
"s = solid ; 1 = l iquid ; g= gas ; aq = dissolved in water at a concentration of I M.