Page 93 - Basics of Fluid Mechanics and Introduction to Computational Fluid Dynamics

78 BASICS OF FLUID MECHANICS AND INTRODUCTION TO CFD

The variables a,b, zp, y'p are related by the relationship a? = yf +
(6 x‘)? and they control the shape of the airfoil. For instance, a and
—
b determine the thickness and the chord length while the ordinate of P
the “camber” of the airfoil.
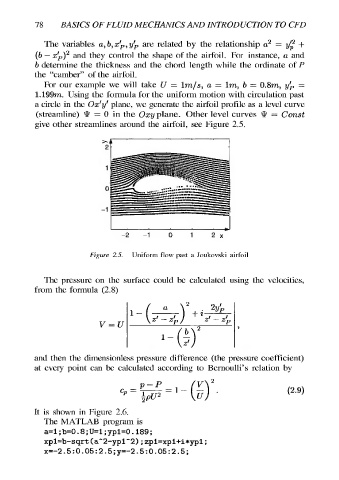
For our example we will take U = 1m/s, a = 1m, b = 0.8m, yp =

1.199m. Using the formula for the uniform motion with circulation past
a circle in the Oz'y’ plane, we generate the airfoil profile as a level curve
(streamline) Y = 0 in the Ozy plane. Other level curves UV = Const
give other streamlines around the airfoil, see Figure 2.5.

>
2

-2 —1 G 1 2 x

Figure 2.5. Uniform flow past a Joukovski airfoil

The pressure on the surface could be calculated using the velocities,

from the formula (2.8)

and then the dimensionless pressure difference (the pressure coefficient)
at every point can be calculated according to Bernoulli’s relation by

V
— pl —]1 __ ? .
2.
t pU? (; ) (2.9)
It is shown in Figure 2.6.
The MATLAB program is

a=1;b=0.8;U=1; yp1=0.189;
xpi=b-sqrt (a*2-yp1°2) ;zpi=xpiti*yp1;
=-2.5:0.05:2.5; y=-2.5:0.05:2.5;