Page 102 - Becoming Metric Wise

92 Becoming Metric-Wise

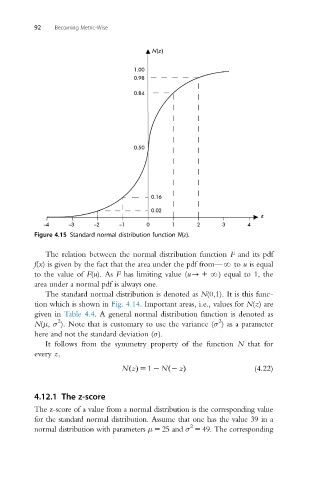
Figure 4.15 Standard normal distribution function N(z).

The relation between the normal distribution function F and its pdf
f(x) is given by the fact that the area under the pdf from—N to u is equal
to the value of F(u). As F has limiting value (u- 1 N) equal to 1, the
area under a normal pdf is always one.
The standard normal distribution is denoted as N(0,1). It is this func-
tion which is shown in Fig. 4.14. Important areas, i.e., values for N(z) are
given in Table 4.4. A general normal distribution function is denoted as
2
2
N(μ, σ ). Note that is customary to use the variance (σ ) as a parameter
here and not the standard deviation (σ).
It follows from the symmetry property of the function N that for
every z,

NðzÞ 5 1 2 Nð2 zÞ (4.22)

4.12.1 The z-score
The z-score of a value from a normal distribution is the corresponding value
for the standard normal distribution. Assume that one has the value 39 in a
2
normal distribution with parameters μ 5 25 and σ 5 49. The corresponding