Page 339 - Biaxial Multiaxial Fatigue and Fracture

Variability in Fatigue Lives: An Effect of the Elastic Anisotropy of Grains? 323

I

1 i d

u
Mar Schmid Factor
ulowwthan s
~
+- greater than s

0.5
0.25 \’

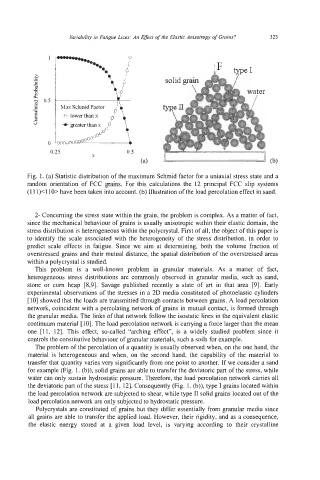
Fig. 1. (a) Statistic distribution of the maximum Schmid factor for a uniaxial stress state and a
random orientation of FCC grains. For this calculations the 12 principal FCC slip systems
(1 11)<1 IO> have been taken into account. (b) Illustration of the load percolation effect in sand.

2- Concerning the stress state within the grain, the problem is complex. As a matter of fact,
since the mechanical behaviour of grains is usually anisotropic within their elastic domain, the
stress distribution is heterogeneous within the polycrystal. First of all, the object of this paper is
to identify the scale associated with the heterogeneity of the stress distribution, in order to
predict scale effects in fatigue. Since we aim at determining, both the volume fraction of
overstressed grains and their mutual distance, the spatial distribution of the overstressed areas
within a polycrystal is studied.
This problem is a well-known problem in granular materials. As a matter of fact,
heterogeneous stress distributions are commonly observed in granular media, such as sand,
stone or corn heap [8,9]. Savage published recently a state of art in that area [9]. Early
experimental observations of the stresses in a 2D media constituted of photoelastic cylinders
[ 101 showed that the loads are transmitted through contacts between grains. A load percolation
network, coincident with a percolating network of grains in mutual contact, is formed through
the granular media. The links of that network follow the isostatic lines in the equivalent elastic
continuum material [IO]. The load percolation network is carrying a force larger than the mean
one [ll, 121. This effect, so-called “arching effect”, is a widely studied problem since it
controls the constitutive behaviour of granular materials, such a soils for example.
The problem of the percolation of a quantity is usually observed when, on the one hand, the
material is heterogeneous and when, on the second hand, the capability of the material to
transfer that quantity varies very significantly from one point to another. If we consider a sand
for example (Fig. 1. (b)), solid grains are able to transfer the deviatoric part of the stress, while
water can only sustain hydrostatic pressure. Therefore, the load percolation network carries all
the deviatoric part of the stress [ 1 I, 121. Consequently (Fig. 1. (b)), type I grains located within
the load percolation network are subjected to shear, while type I1 solid grains located out of the
load percolation network are only subjected to hydrostatic pressure.
Polycrystals are constituted of grains but they differ essentially from granular media since
all grains are able to transfer the applied load. However, their rigidity, and as a consequence,
the elastic energy stored at a given load level, is varying according to their crystalline