Page 124 - Biodegradable Polyesters

102 4 Synthesis, Properties, and Mathematical Modeling of Biodegradable Aliphatic Polyesters

Furthermore, the number average molecular weight is expressed as
2
M = [COOH]+[OH] (4.41)
n
Then, Equations 4.39–4.41 and the Berkowitz equation M = 3.29 × 10 [ ] 1.54
4
n
constitute a set of ordinary differential equations which can be easily solved
numerically using a varying step-size Runge–Kutta method to give intrinsic vis-
cosity, as well as concentration of hydroxyl and carboxyl end groups as a function
of time. Four adjustable parameters, namely, k , k ,[OH] , and [COOH] ,are
1
i
2
i
estimated at each temperature and glycol used by simultaneous fitting of the
values of all three variables to the experimental data points as a function of time.
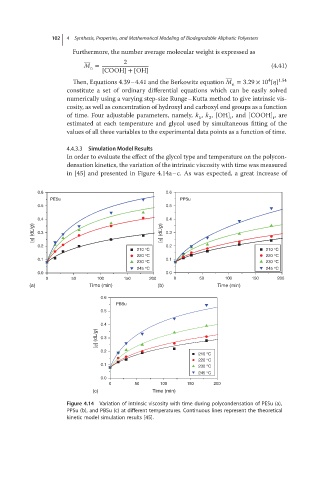
4.4.3.3 Simulation Model Results
In order to evaluate the effect of the glycol type and temperature on the polycon-
densation kinetics, the variation of the intrinsic viscosity with time was measured
in [45] and presented in Figure 4.14a–c. As was expected, a great increase of

0.6 0.6
PESu PPSu
0.5 0.5
0.4 0.4
[η] (dL/g) 0.3 [η] (dL/g) 0.3

0.2 0.2
210 °C 210 °C
220 °C 220 °C
0.1 0.1
230 °C 230 °C
245 °C 245 °C
0.0 0.0
0 50 100 150 200 0 50 100 150 200
(a) Time (min) (b) Time (min)
0.6
PBSu
0.5
0.4
[η] (dL/g) 0.3

0.2
210 °C
220 °C
0.1 230 °C
245 °C
0.0
0 50 100 150 200
(c) Time (min)
Figure 4.14 Variation of intrinsic viscosity with time during polycondensation of PESu (a),
PPSu (b), and PBSu (c) at different temperatures. Continuous lines represent the theoretical
kinetic model simulation results [45].