Page 105 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

82 BIOMECHANICS OF THE HUMAN BODY

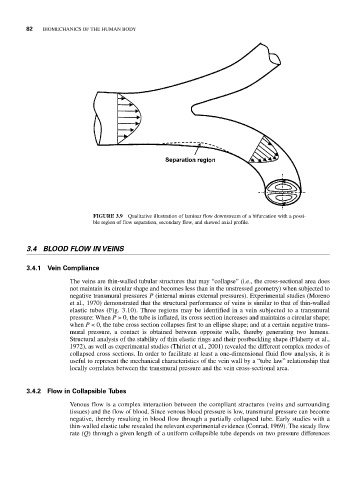
FIGURE 3.9 Qualitative illustration of laminar flow downstream of a bifurcation with a possi-
ble region of flow separation, secondary flow, and skewed axial profile.

3.4 BLOOD FLOW IN VEINS

3.4.1 Vein Compliance
The veins are thin-walled tubular structures that may “collapse” (i.e., the cross-sectional area does
not maintain its circular shape and becomes less than in the unstressed geometry) when subjected to
negative transmural pressures P (internal minus external pressures). Experimental studies (Moreno
et al., 1970) demonstrated that the structural performance of veins is similar to that of thin-walled
elastic tubes (Fig. 3.10). Three regions may be identified in a vein subjected to a transmural
pressure: When P > 0, the tube is inflated, its cross section increases and maintains a circular shape;
when P < 0, the tube cross section collapses first to an ellipse shape; and at a certain negative trans-
mural pressure, a contact is obtained between opposite walls, thereby generating two lumens.
Structural analysis of the stability of thin elastic rings and their postbuckling shape (Flaherty et al.,
1972), as well as experimental studies (Thiriet et al., 2001) revealed the different complex modes of
collapsed cross sections. In order to facilitate at least a one-dimensional fluid flow analysis, it is
useful to represent the mechanical characteristics of the vein wall by a “tube law” relationship that
locally correlates between the transmural pressure and the vein cross-sectional area.

3.4.2 Flow in Collapsible Tubes

Venous flow is a complex interaction between the compliant structures (veins and surrounding
tissues) and the flow of blood. Since venous blood pressure is low, transmural pressure can become
negative, thereby resulting in blood flow through a partially collapsed tube. Early studies with a
thin-walled elastic tube revealed the relevant experimental evidence (Conrad, 1969). The steady flow
rate (Q) through a given length of a uniform collapsible tube depends on two pressure differences