Page 106 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

PHYSICAL AND FLOW PROPERTIES OF BLOOD 83

selected from among the pressures immediately
upstream (P ), immediately downstream (P ), and
1
2
external (P ) to the collapsible segment (Fig. 3.11).
e
Thus, the pressure-flow relationships in col-
lapsible tubes are more complex than those of
rigid tubes, where Q is related to a fixed pres-
sure gradient, and may attain different shapes,
depending on which of the pressures (e.g., P ,
1
P , P ) are held fixed and which are varied. In
2
e
addition, one should also consider the facts that
real veins may be neither uniform nor straight,
and that the external pressure is not necessarily
uniform along the tube.
The one-dimensional theory for steady
incompressible fluid flow in collapsible tubes
(when P − P < 0) was outlined by Shapiro
e
(1977) in a format analogous to that for gas
dynamics. The governing equations for the fluid
are that for conservation of mass,
∂A ∂
+ ( Au) = 0
∂t ∂z (3.39)
and that for conservation of momentum,
∂u ∂u 1 ∂P
+ u =− (3.40)
∂t ∂z ρ ∂z
where u = velocity
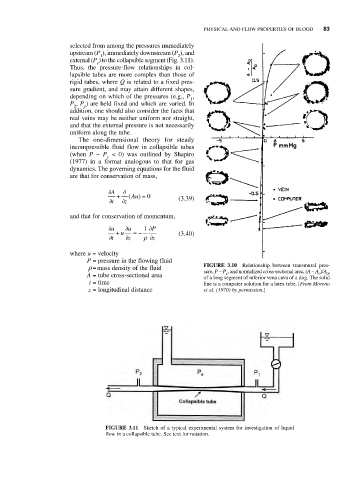
P = pressure in the flowing fluid FIGURE 3.10 Relationship between transmural pres-
r =mass density of the fluid sure, P − P , and normalized cross-sectional area, (A − A )/A ,
A = tube cross-sectional area of a long segment of inferior vena cava of a dog. The solid 0
0
e
t = time line is a computer solution for a latex tube. [From Moreno
z = longitudinal distance et al. (1970) by permission.]

FIGURE 3.11 Sketch of a typical experimental system for investigation of liquid
flow in a collapsible tube. See text for notation.