Page 42 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals
P. 42
MODELING OF BIOMEDICAL SYSTEMS 19
42.42
A
33.94
Production rate 25.45
16.97
8.48
0.00
0.00 0.80 1.60 2.40 3.20 4.00 4.80 5.60 6.40 7.20 8.00
Time in days
0.85
B
0.68
Target cells 0.51
0.34
0.17
0.00
0.00 0.80 1.60 2.40 3.20 4.00 4.80 5.60 6.40 7.20 8.00
Time in days
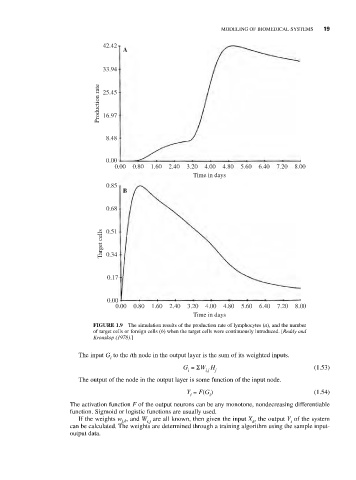
FIGURE 1.9 The simulation results of the production rate of lymphocytes (a), and the number
of target cells or foreign cells (b) when the target cells were continuously introduced. [Reddy and
Krouskop (1978).]
The input G to the ith node in the output layer is the sum of its weighted inputs.
i
G =ΣW H (1.53)
i i,j j
The output of the node in the output layer is some function of the input node.
Y = F(G ) (1.54)
i i
The activation function F of the output neurons can be any monotone, nondecreasing differentiable
function. Sigmoid or logistic functions are usually used.
If the weights w j,k , and W are all known, then given the input X , the output Y of the system
i,j k i
can be calculated. The weights are determined through a training algorithm using the sample input-
output data.