Page 45 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

22 BIOMEDICAL SYSTEMS ANALYSIS

1.6 FUZZY LOGIC

Most real world systems include some element of uncertainty and cannot be accurately modeled
using crisp logic. Moreover, some of these systems require modeling of parameters like human expe-
rience, intuition, etc., which involve various degrees of conceptual uncertainties and vagueness.
Several of these applications require fuzzy definition of boundaries and fuzzy classes, whose mem-
bership values are in the form of degree of membership, rather than in the form of true or false. In
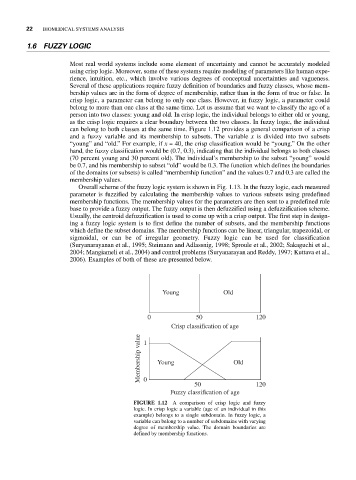
crisp logic, a parameter can belong to only one class. However, in fuzzy logic, a parameter could
belong to more than one class at the same time. Let us assume that we want to classify the age of a
person into two classes: young and old. In crisp logic, the individual belongs to either old or young,
as the crisp logic requires a clear boundary between the two classes. In fuzzy logic, the individual
can belong to both classes at the same time. Figure 1.12 provides a general comparison of a crisp
and a fuzzy variable and its membership to subsets. The variable x is divided into two subsets
“young” and “old.” For example, if x = 40, the crisp classification would be “young.” On the other
hand, the fuzzy classification would be (0.7, 0.3), indicating that the individual belongs to both classes
(70 percent young and 30 percent old). The individual’s membership to the subset “young” would
be 0.7, and his membership to subset “old” would be 0.3. The function which defines the boundaries
of the domains (or subsets) is called “membership function” and the values 0.7 and 0.3 are called the
membership values.
Overall scheme of the fuzzy logic system is shown in Fig. 1.13. In the fuzzy logic, each measured
parameter is fuzzified by calculating the membership values to various subsets using predefined
membership functions. The membership values for the parameters are then sent to a predefined rule
base to provide a fuzzy output. The fuzzy output is then defuzzified using a defuzzification scheme.
Usually, the centroid defuzzification is used to come up with a crisp output. The first step in design-
ing a fuzzy logic system is to first define the number of subsets, and the membership functions
which define the subset domains. The membership functions can be linear, triangular, trapezoidal, or
sigmoidal, or can be of irregular geometry. Fuzzy logic can be used for classification
(Suryanarayanan et al., 1995; Steimann and Adlassnig, 1998; Sproule et al., 2002; Sakaguchi et al.,
2004; Mangiameli et al., 2004) and control problems (Suryanarayan and Reddy, 1997; Kuttava et al.,
2006). Examples of both of these are presented below.

Young Old

0 50 120
Crisp classification of age
Membership value 1 Young Old

0
50 120
Fuzzy classification of age
FIGURE 1.12 A comparison of crisp logic and fuzzy
logic. In crisp logic a variable (age of an individual in this
example) belongs to a single subdomain. In fuzzy logic, a
variable can belong to a number of subdomains with varying
degree of membership value. The domain boundaries are
defined by membership functions.