Page 295 - Biomedical Engineering and Design Handbook Volume 2, Applications

THE PRINCIPLES OF X-RAY COMPUTED TOMOGRAPHY 273

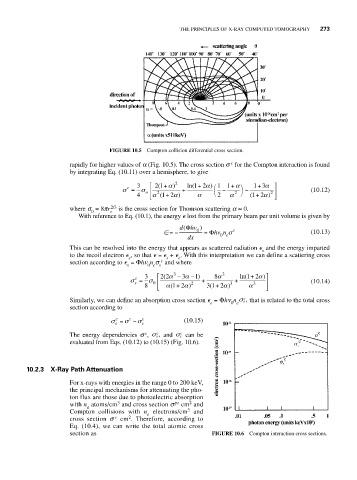
FIGURE 10.5 Compton collision differential cross section.
c
rapidly for higher values of a (Fig. 10.5). The cross section s for the Compton interaction is found
by integrating Eq. (10.11) over a hemisphere, to give
+
+
α ⎛ 1 1
c
σ = 3 σ o ⎢ ⎡ 21 ( + α) 2 + ln( 12 ) − + 2 α ⎞ − 13α 2 ⎤ ⎥ (10.12)
2
+
+
4 ⎣ α 12 α) α ⎝ 2 α ⎠ ⎠ ( 12α) ⎦
(
where s = 8pr 2/3 is the cross section for Thomson scattering a ≈ 0.
0 e
With reference to Eq. (10.1), the energy lost from the primary beam per unit volume is given by
d(Φ hv )
∈=− 0 = hv n σ c (10.13)
Φ
dx 0 e
This can be resolved into the energy that appears as scattered radiation and the energy imparted
s
to the recoil electron , so that = + . With this interpretation we can define a scattering cross
e
e
s
c
section according to =Φhn n s and where
s 0 e s
3
+
3 ⎡ 22 ( α − 3 α −1) 8 α 2 ln(112α) ⎤
c
σ = σ 0 ⎢ 2 + 3 + 3 ⎥ (10.14)
s
12
(
8 ⎣ α + α) 31 ( + 2 α) α ⎦
c
Similarly, we can define an absorption cross section =Φhn n σ e , that is related to the total cross
e 0 e
section according to
c
c
σ = σ − σ s c (10.15)
e
c
c
The energy dependencies s , σ s , and σ e c can be
evaluated from Eqs. (10.12) to (10.15) (Fig. 10.6).
10.2.3 X-Ray Path Attenuation
For x-rays with energies in the range 0 to 200 keV,
the principal mechanisms for attenuating the pho-
ton flux are those due to photoelectric absorption
with n atoms/cm and cross section s pe cm and
3
2
a
3
Compton collisions with n electrons/cm and
e
2
cross section s c cm . Therefore, according to
Eq. (10.4), we can write the total atomic cross
section as FIGURE 10.6 Compton interaction cross sections.