Page 171 - Buried Pipe Design

Design of Gravity Flow Pipes 145

represented fairly accurately with a bilinear curve. A modulus correc-
tion that will produce the desired results is as follows:
The effective modulus is actually a soil-structure interaction term
and is dependent on both the soil and the pipe. Thus, the break point
may be different for different pipe products.

2.5 E′ H b
E′ eff H b
2.5 E′H
[b 2.5 (H b)]

E′ eff effective soil modulus
E′ traditional soil modulus
H height of cover
b break height (where the curve changes slope)

Proctor density, percent Soil modulus E′ Break point b
2
80 1.73–3.45 MPa (250–500 lb/in ) 1 m (3 ft)
2
85 3.45–4.82 MPa (500–700 lb/in ) 1.5 m (5 ft)
2
90 4.82–6.89 MPa (700–1000 lb/in ) 3 m (10 ft)
2
97 6.89–11.02 MPa (1000–1600 lb/in ) 9 m (30 ft)
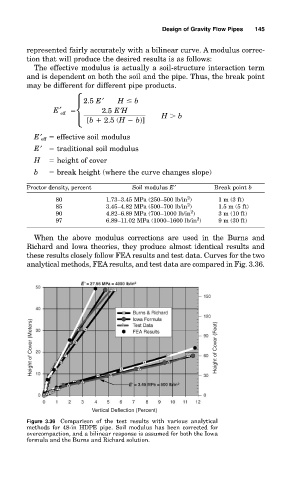
When the above modulus corrections are used in the Burns and
Richard and Iowa theories, they produce almost identical results and
these results closely follow FEA results and test data. Curves for the two
analytical methods, FEA results, and test data are compared in Fig. 3.36.

E

Height of Cover (Meters) Height of Cover (Feet)

E

Vertical Deflection (Percent)
Figure 3.36 Comparison of the test results with various analytical
methods for 48-in HDPE pipe. Soil modulus has been corrected for
overcompaction, and a bilinear response is assumed for both the Iowa
formula and the Burns and Richard solution.