Page 194 - Calculus Workbook For Dummies

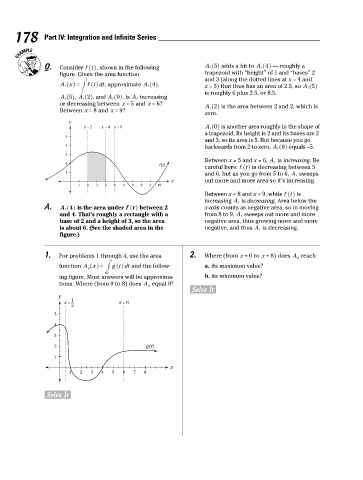
178 Part IV: Integration and Infinite Series

Q. Consider f t ^ h, shown in the following A 5 ^ h adds a bit to A 4 ^ h — roughly a
f
f
figure. Given the area function trapezoid with “height” of 1 and “bases” 2
x and 3 (along the dotted lines at x = 4 and
A x = # ^h f t dt, approximate A 4 ^ h, x = 5) that thus has an area of 2.5, so A 5 ^ h
f ^
h
f
f
2 is roughly 6 plus 2.5, or 8.5.
A 5 ^ h, A 2 ^ h, and A 0 ^ h. Is A f increasing
f
f
f
or decreasing between x = 5 and x = 6? A 2 ^ h is the area between 2 and 2, which is
Between x = 8 and x = 9? f
zero.
y
x = 2 x = 4 x = 5 A 0 ^ h is another area roughly in the shape of
f
a trapezoid. Its height is 2 and its bases are 2
5
and 3, so its area is 5. But because you go
4
backwards from 2 to zero, A 0 ^ h equals –5.
f
3
Between x = 5 and x = 6, A f is increasing. Be
2
f (t)
careful here: f t ^ h is decreasing between 5
1
and 6, but as you go from 5 to 6, A f sweeps
x out more and more area so it’s increasing.
1 2 3 4 5 6 7 8 9 10
Between x = 8 and x = 9, while f t ^ h is
increasing A f is decreasing. Area below the
A. A 4h is the area under f t ^ h between 2 x-axis counts as negative area, so in moving
f ^
and 4. That’s roughly a rectangle with a from 8 to 9, A f sweeps out more and more
base of 2 and a height of 3, so the area negative area, thus growing more and more
is about 6. (See the shaded area in the negative, and thus A f is decreasing.
figure.)
1. For problems 1 through 4, use the area 2. Where (from x = 0 to x = 8) does A g reach
x
function A x = # ^h g t dt and the follow- a. its maximum value?
g^
h
/ 1 2
ing figure. Most answers will be approxima- b. its minimum value?
tions. Where (from 0 to 8) does A g equal 0?
Solve It
y
x = 1 x = 6
2
5
4
3
2 g (t)
1
x
1 2 3 4 5 6 7 8

Solve It