Page 94 - Cam Design Handbook

THB3 8/15/03 12:58 PM Page 82

82 CAM DESIGN HANDBOOK

The displacement, velocity, and acceleration characteristics of the curves are indicated.
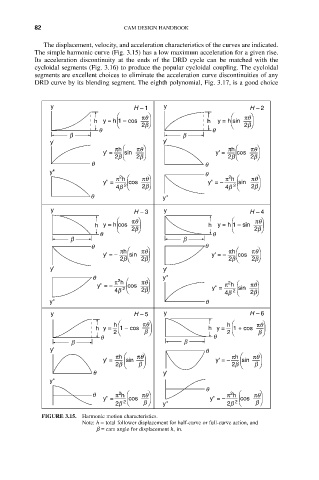
The simple harmonic curve (Fig. 3.15) has a low maximum acceleration for a given rise.
Its acceleration discontinuity at the ends of the DRD cycle can be matched with the
cycloidal segments (Fig. 3.16) to produce the popular cycloidal coupling. The cycloidal
segments are excellent choices to eliminate the acceleration curve discontinuities of any
DRD curve by its blending segment. The eighth polynomial, Fig. 3.17, is a good choice

y H – 1 y H – 2
Ê pqˆ Ê pqˆ
Á
Á
h y = h 1 – cos ˜ h y = h sin ˜
Ë 2b¯ Ë 2b¯
q q
b b
y' y'
ph Ê pqˆ ph Ê pqˆ
Á
Á
y' = sin ˜ y' = cos ˜
2b Ë 2b¯ 2b Ë 2b¯
q q
y" q
2
2
p h Ê pqˆ p h Ê pqˆ
Á
y" = cos ˜ y" = – sin ˜
2 Á
2
4b Ë 2b¯ 4b Ë 2b¯
q y"
y H – 3 y H – 4
Ê pqˆ Ê pqˆ
Á
h y = h cos ˜ h y = h 1 – sin ˜
Á
Ë 2b¯ Ë 2b¯
q q
b b
q ph Ê pqˆ q ph Ê pqˆ
Á
Á
y' = – sin ˜ y' = – cos ˜
2b Ë 2b ¯ 2b Ë 2b¯
y' y'
q p h Ê pq ˆ y"
2
pqˆ
p h Ê
2
y" = – cos ˜ y" = sin ˜
Á
2 Á
2
4b Ë 2b ¯ 4b Ë 2b ¯
y" q
y H – 5 y H – 6
h Ê pqˆ h Ê pq ˆ
Á
Á
h y = 1 – cos ˜ h y = 1 + cos ˜
2 Ë b ¯ 2 Ë b¯
q q
b b
y' q
ph Ê pqˆ ph Ê pqˆ
Á
y' = sin ˜ y' = – sin ˜
Á
2b Ë b ¯ 2b Ë b ¯
q y'
y"
q
2
2
q p h Ê pq ˆ p h Ê pq ˆ
Á
y" = cos ˜ y" = – cos ˜
Á
2
2b Ë b¯ y" 2b Ë b¯
2
FIGURE 3.15. Harmonic motion characteristics.
Note: h = total follower displacement for half-curve or full-curve action, and
b = cam angle for displacement h, in.