Page 92 - Cam Design Handbook

THB3 8/15/03 12:58 PM Page 80

80 CAM DESIGN HANDBOOK

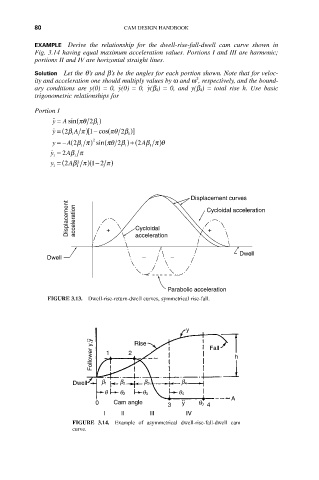
EXAMPLE Derive the relationship for the dwell-rise-fall-dwell cam curve shown in
Fig. 3.14 having equal maximum acceleration values. Portions I and III are harmonic;
portions II and IV are horizontal straight lines.
Solution Let the q’s and b’s be the angles for each portion shown. Note that for veloc-
2
ity and acceleration one should multiply values by w and w , respectively, and the bound-
˙ y
˙ y
ary conditions are y(0) = 0, (0) = 0, (b 4 ) = 0, and y(b 4 ) = total rise h. Use basic
trigonometric relationships for
Portion I
˙˙ y = A sin(pq 2 b )
1
p
[1
˙ y = ( b2 A ) - cos(pq 2 b )]
1 1
y =- A( bp2 1 ) 2 sin(pq 2 b 1 )+ (2 Abp )q
1
˙ y = 2 Abp
1 1
2
y = (2 Abp ) - 2 p )
(1
1 1
Displacement curves
Displacement acceleration + Cycloidal Cycloidal acceleration

+
acceleration

Dwell
Dwell – –

Parabolic acceleration
FIGURE 3.13. Dwell-rise-return-dwell curves, symmetrical rise-fall.

y
Follower y,y 1 2 Rise Fall h

Dwell b 1 b 2 b 3 b 4
q q 2 q 3 q 4
A
0 Cam angle 3 y q 0 4
I II III IV
FIGURE 3.14. Example of asymmetrical dwell-rise-fall-dwell cam
curve.