Page 72 - Characterization and Properties of Petroleum Fractions

P2: —/—
QC: —/—
P1: KVU/—
AT029-Manual-v7.cls
AT029-02
AT029-Manual
52 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
Reduced Boiling Point, Tbr T1: IML August 16, 2007 16:6

Molecular Weight
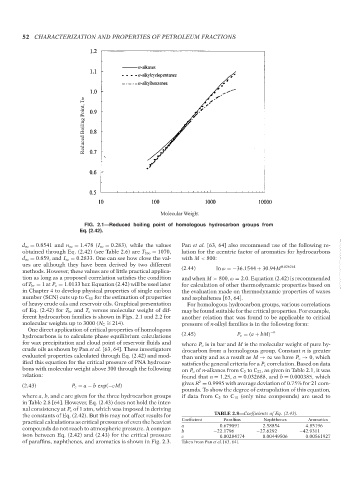
FIG. 2.1—Reduced boiling point of homologous hydrocarbon groups from
Eq. (2.42).

d ∞ = 0.8541 and n ∞ = 1.478 (I ∞ = 0.283), while the values Pan et al. [63, 64] also recommend use of the following re-
obtained through Eq. (2.42) (see Table 2.6) are T b∞ = 1070, lation for the acentric factor of aromatics for hydrocarbons
d ∞ = 0.859, and I ∞ = 0.2833. One can see how close the val- with M < 800:
ues are although they have been derived by two different 0.026261 --`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
methods. However, these values are of little practical applica- (2.44) ln ω =−36.1544 + 30.94M
tion as long as a proposed correlation satisfies the condition and when M > 800, ω = 2.0. Equation (2.42) is recommended
of T br = 1at P c = 1.0133 bar. Equation (2.42) will be used later for calculation of other thermodynamic properties based on
in Chapter 4 to develop physical properties of single carbon the evaluation made on thermodynamic properties of waxes
number (SCN) cuts up to C 50 for the estimation of properties and asphaltenes [63, 64].
of heavy crude oils and reservoir oils. Graphical presentation For homologous hydrocarbon groups, various correlations
of Eq. (2.42) for T br and T c versus molecular weight of dif- may be found suitable for the critical properties. For example,
ferent hydrocarbon families is shown in Figs. 2.1 and 2.2 for another relation that was found to be applicable to critical
molecular weights up to 3000 (N C = 214). pressure of n-alkyl families is in the following form:
∼
One direct application of critical properties of homologous −n
hydrocarbons is to calculate phase equilibrium calculations (2.45) P c = (a + bM)
for wax precipitation and cloud point of reservoir fluids and where P c is in bar and M is the molecular weight of pure hy-
crude oils as shown by Pan et al. [63, 64]. These investigators drocarbon from a homologous group. Constant n is greater
evaluated properties calculated through Eq. (2.42) and mod- than unity and as a result as M →∞ we have P c → 0, which
ified this equation for the critical pressure of PNA hydrocar- satisfies the general criteria for a P c correlation. Based on data
bons with molecular weight above 300 through the following on P c of n-alkanes from C 2 to C 22 , as given in Table 2.1, it was
relation: found that n = 1.25, a = 0.032688, and b = 0.000385, which
2
gives R = 0.9995 with average deviation of 0.75% for 21 com-
(2.43) P c = a − b exp(−cM)
pounds. To show the degree of extrapolation of this equation,
where a, b, and c are given for the three hydrocarbon groups if data from C 2 to C 10 (only nine compounds) are used to
in Table 2.8 [64]. However, Eq. (2.43) does not hold the inter-
nal consistency at P c of 1 atm, which was imposed in deriving
the constants of Eq. (2.42). But this may not affect results for TABLE 2.8—Coefficients of Eq. (2.43).
practical calculations as critical pressures of even the heaviest Coefficient Paraffins Naphthenes Aromatics
0.679091
2.58854
4.85196
compounds do not reach to atmospheric pressure. A compar- a b −22.1796 −27.6292 −42.9311
ison between Eq. (2.42) and (2.43) for the critical pressure c 0.00284174 0.00449506 0.00561927
of paraffins, naphthenes, and aromatics is shown in Fig. 2.3. Taken from Pan et al. [63, 64].

Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT