Page 157 - Civil Engineering Formulas
P. 157
COLUMN FORMULAS 95
where E modulus of elasticity of the column material, psi (Mpa)
2
2
A column cross-sectional area, in (mm )
r radius of gyration of the column, in (mm)
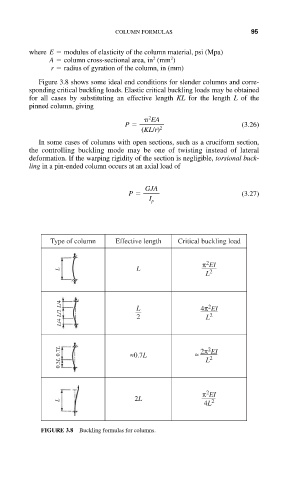
Figure 3.8 shows some ideal end conditions for slender columns and corre-
sponding critical buckling loads. Elastic critical buckling loads may be obtained
for all cases by substituting an effective length KL for the length L of the
pinned column, giving
2
EA
P (3.26)
(KL/r) 2
In some cases of columns with open sections, such as a cruciform section,
the controlling buckling mode may be one of twisting instead of lateral
deformation. If the warping rigidity of the section is negligible, torsional buck-
ling in a pin-ended column occurs at an axial load of
GJA
P (3.27)
I p
Type of column Effective length Critical buckling load
2
π EI
L L 2
L
L/4 L 4π EI
2
L/2 2 L 2
L/4
0.7L ~ ~ ~ 2π EI
2
~0.7L
0.3L L 2
2
π EI
2L
L 2
4L
FIGURE 3.8 Buckling formulas for columns.