Page 180 - Computational Colour Science Using MATLAB

COMPUTATIONAL COLOUR CONSTANCY AND LINEAR MODELS 167

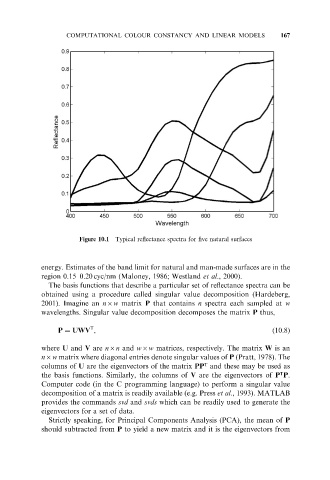
Figure 10.1 Typical reflectance spectra for five natural surfaces

energy. Estimates of the band limit for natural and man-made surfaces are in the
region 0.15–0.20 cyc/nm (Maloney, 1986; Westland et al., 2000).
The basis functions that describe a particular set of reflectance spectra can be
obtained using a procedure called singular value decomposition (Hardeberg,
2001). Imagine an n6w matrix P that contains n spectra each sampled at w
wavelengths. Singular value decomposition decomposes the matrix P thus,

T
P ¼ UWV , ð10.8Þ
where U and V are n6n and w6w matrices, respectively. The matrix W is an
n6w matrix where diagonal entries denote singular values of P (Pratt, 1978). The
T
columns of U are the eigenvectors of the matrix PP and these may be used as
the basis functions. Similarly, the columns of V are the eigenvectors of P P.
T
Computer code (in the C programming language) to perform a singular value
decomposition of a matrix is readily available (e.g. Press et al., 1993). MATLAB
provides the commands svd and svds which can be readily used to generate the
eigenvectors for a set of data.
Strictly speaking, for Principal Components Analysis (PCA), the mean of P
should subtracted from P to yield a new matrix and it is the eigenvectors from