Page 334 - Computational Statistics Handbook with MATLAB

Chapter 9: Statistical Pattern Recognition 323

Iris Virginica

1.2
1
0.8
0.6
0.4
0.2

3.5
8
3 7
2.5 6
5
Sepal Width Sepal Length

IG
FI F U URE G 9. RE 9. 2 2
GU
2
F F II GU RE RE 9. 9. 2
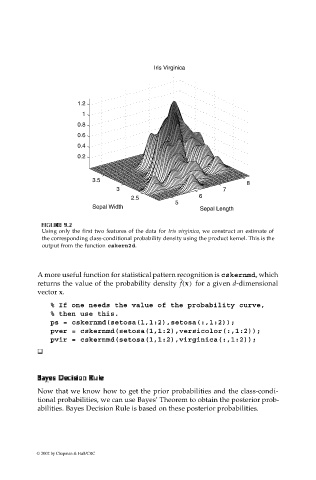
Using only the first two features of the data for Iris virginica, we construct an estimate of
the corresponding class-conditional probability density using the product kernel. This is the
output from the function cskern2d.
A more useful function for statistical pattern recognition is cskernmd, which
ˆ
returns the value of the probability density f x() for a given d-dimensional
vector x.
% If one needs the value of the probability curve,
% then use this.
ps = cskernmd(setosa(1,1:2),setosa(:,1:2));
pver = cskernmd(setosa(1,1:2),versicolor(:,1:2));
pvir = cskernmd(setosa(1,1:2),virginica(:,1:2));

ule
Ba
BBaayeye
Bayeye s ss sDDe ecisioncisionR RR uleule
R
DDeecisioncision
ule
Now that we know how to get the prior probabilities and the class-condi-
tional probabilities, we can use Bayes’ Theorem to obtain the posterior prob-
abilities. Bayes Decision Rule is based on these posterior probabilities.

© 2002 by Chapman & Hall/CRC