Page 56 - Computational Statistics Handbook with MATLAB

42 Computational Statistics Handbook with MATLAB

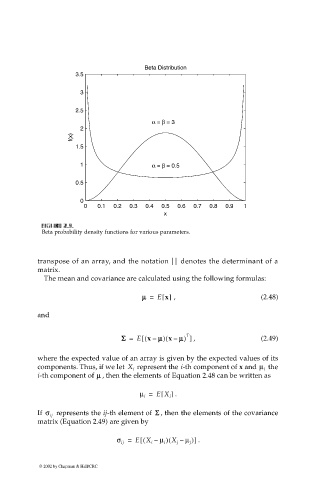
Beta Distribution
3.5

3

2.5
α = β = 3
2
f(x)
1.5

1 α = β = 0.5

0.5

0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
x

GU
F FI F F IG URE G 2.9. RE RE RE 2.9. 2.9. 2.9.
U
II
GU
Beta probability density functions for various parameters.
transpose of an array, and the notation | | denotes the determinant of a
matrix.
The mean and covariance are calculated using the following formulas:

µ µ µ µ = E x[] , (2.48)

and

( [
µ µ µ µ
(
Σ Σ Σ Σ = E x – ) x – µ µ µ µ) T , ] (2.49)
where the expected value of an array is given by the expected values of its
the
components. Thus, if we let X i represent the i-th component of x and µ i
µ µ µ µ
i-th component of , then the elements of Equation 2.48 can be written as
[
µ i = EX i . ]
Σ Σ Σ Σ
represents the ij-th element of , then the elements of the covariance
If σ ij
matrix (Equation 2.49) are given by
[
(
σ ij = EX i – µ i ) X j –( µ j )] .

© 2002 by Chapman & Hall/CRC