Page 153 -

132 3 Image processing

1 Linear
Binomial
Cubic a=-1
0.8
Cubic a=-0.5
Wind. sinc
0.6
QMF-9
JPEG 2000
0.4

0.2

0
0 0.1 0.2 0.3 0.4 0.5
-0.2

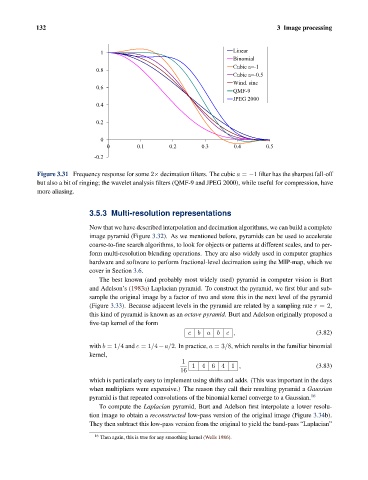
Figure 3.31 Frequency response for some 2× decimation filters. The cubic a = −1 filter has the sharpest fall-off
but also a bit of ringing; the wavelet analysis filters (QMF-9 and JPEG 2000), while useful for compression, have
more aliasing.

3.5.3 Multi-resolution representations

Now that we have described interpolation and decimation algorithms, we can build a complete
image pyramid (Figure 3.32). As we mentioned before, pyramids can be used to accelerate
coarse-to-fine search algorithms, to look for objects or patterns at different scales, and to per-
form multi-resolution blending operations. They are also widely used in computer graphics
hardware and software to perform fractional-level decimation using the MIP-map, which we
cover in Section 3.6.
The best known (and probably most widely used) pyramid in computer vision is Burt
and Adelson’s (1983a) Laplacian pyramid. To construct the pyramid, we first blur and sub-
sample the original image by a factor of two and store this in the next level of the pyramid
(Figure 3.33). Because adjacent levels in the pyramid are related by a sampling rate r =2,
this kind of pyramid is known as an octave pyramid. Burt and Adelson originally proposed a
five-tap kernel of the form
c b a b c , (3.82)

with b =1/4 and c =1/4−a/2. In practice, a =3/8, which results in the familiar binomial
kernel,
1
1 4 6 4 1 , (3.83)
16
which is particularly easy to implement using shifts and adds. (This was important in the days
when multipliers were expensive.) The reason they call their resulting pyramid a Gaussian
pyramid is that repeated convolutions of the binomial kernel converge to a Gaussian. 16
To compute the Laplacian pyramid, Burt and Adelson first interpolate a lower resolu-
tion image to obtain a reconstructed low-pass version of the original image (Figure 3.34b).
They then subtract this low-pass version from the original to yield the band-pass “Laplacian”

16 Then again, this is true for any smoothing kernel (Wells 1986).