Page 157 -

136 3 Image processing

coarse l = 4 coarse l = 2
l = 3
medium l = 2 medium l = 1

l = 1

fine l = 0 fine l = 0

(a) (b)

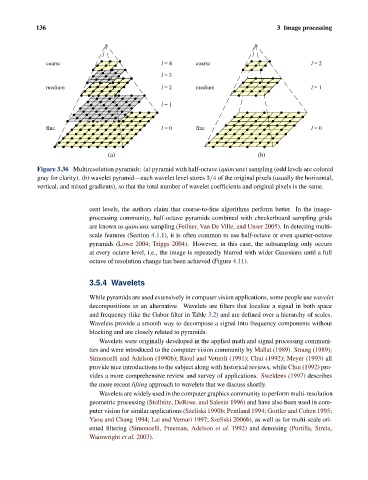
Figure 3.36 Multiresolution pyramids: (a) pyramid with half-octave (quincunx) sampling (odd levels are colored
gray for clarity). (b) wavelet pyramid—each wavelet level stores 3/4 of the original pixels (usually the horizontal,
vertical, and mixed gradients), so that the total number of wavelet coefficients and original pixels is the same.

cent levels, the authors claim that coarse-to-fine algorithms perform better. In the image-
processing community, half-octave pyramids combined with checkerboard sampling grids
are known as quincunx sampling (Feilner, Van De Ville, and Unser 2005). In detecting multi-
scale features (Section 4.1.1), it is often common to use half-octave or even quarter-octave
pyramids (Lowe 2004; Triggs 2004). However, in this case, the subsampling only occurs
at every octave level, i.e., the image is repeatedly blurred with wider Gaussians until a full
octave of resolution change has been achieved (Figure 4.11).

3.5.4 Wavelets

While pyramids are used extensively in computer vision applications, some people use wavelet
decompositions as an alternative. Wavelets are filters that localize a signal in both space
and frequency (like the Gabor filter in Table 3.2) and are defined over a hierarchy of scales.
Wavelets provide a smooth way to decompose a signal into frequency components without
blocking and are closely related to pyramids.
Wavelets were originally developed in the applied math and signal processing communi-
ties and were introduced to the computer vision community by Mallat (1989). Strang (1989);
Simoncelli and Adelson (1990b); Rioul and Vetterli (1991); Chui (1992); Meyer (1993) all
provide nice introductions to the subject along with historical reviews, while Chui (1992) pro-
vides a more comprehensive review and survey of applications. Sweldens (1997) describes
the more recent lifting approach to wavelets that we discuss shortly.
Wavelets are widely used in the computer graphics community to perform multi-resolution
geometric processing (Stollnitz, DeRose, and Salesin 1996) and have also been used in com-
puter vision for similar applications (Szeliski 1990b; Pentland 1994; Gortler and Cohen 1995;
Yaou and Chang 1994; Lai and Vemuri 1997; Szeliski 2006b), as well as for multi-scale ori-
ented filtering (Simoncelli, Freeman, Adelson et al. 1992) and denoising (Portilla, Strela,
Wainwright et al. 2003).